某初级中学共有学生2000名,各年级男、女生人数如下表:
| |
初一年级 |
初二年级 |
初三年级 |
| 女生 |
373 |
x |
y |
| 男生 |
377 |
370 |
z |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1) 求x的值.
(2) 现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3) 已知y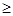 245,z
245,z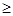 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率.
(请考生在下面甲、乙两题中任选一题做答,如果多做,则按所做的甲题计分)
甲题:
⑴若关于 的不等式
的不等式 的解集不是空集,求实数
的解集不是空集,求实数 的取值范围;
的取值范围;
⑵已知实数 ,满足
,满足 ,求
,求 最小值.
最小值.
乙题:
已知曲线C的极坐标方程是 =4cos
=4cos 。以极点为平面直角坐标系的原点,极轴为
。以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (
( 是参数)。
是参数)。
⑴将曲线C的极坐标方程化成直角坐标方程并把直线 的参数方程转化为普通方程;
的参数方程转化为普通方程;
⑵若过定点 的直线
的直线 与曲线C相交于A、B两点,且
与曲线C相交于A、B两点,且 ,试求实数
,试求实数 的值。
的值。
若实数
(1)若 >2,求函数
>2,求函数 的单调区间;
的单调区间;
(2)若在区间 的取值范围.
的取值范围.
已知函数 ,
,
(1)若 ,求
,求 的值;
的值;
(2)若 对于
对于 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f (t)表示学生注意力随时间t(分钟)的变化规律(f(t)越大,表明学生注意力越集中),经过实验分析得知:
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
设全集为R,集合 ,
, ,
,
(1)求 ;(2)若
;(2)若 ,求
,求 的取值范围
的取值范围