设函数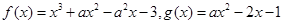 ,其中实数
,其中实数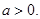
(1)求函数 的单调区间;
的单调区间;
(2)若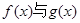 在区间
在区间 上均为增函数,求a的取值范围。
上均为增函数,求a的取值范围。
如图,已知四边形ABCD是菱形,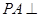 平面ABCD,PA=AB=BD=2,AC与BD交于E点,F是PD的中点。
平面ABCD,PA=AB=BD=2,AC与BD交于E点,F是PD的中点。
(1)求证:PB//平面AFC;
(2)求多面体PABCF的体积。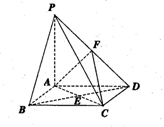
乳制品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5。现从一批该乳制品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
(1)若所抽取的20件乳制品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为4的乳制品记为 ,等级系数为5的乳制品记为
,等级系数为5的乳制品记为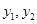 ,现从这5件乳制品
,现从这5件乳制品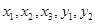 中任取两件(假定每件乳制品被取出的可能性相同),写出所有可能的结果,并求这两件乳制品的等级系数恰好相同的概率
中任取两件(假定每件乳制品被取出的可能性相同),写出所有可能的结果,并求这两件乳制品的等级系数恰好相同的概率
已知向量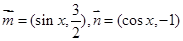 ,设
,设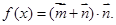
(1)求函数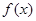 的表达式,并求
的表达式,并求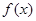 的单调递减区间;
的单调递减区间;
(2)在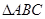 中,a,b,c分别是角A,B,C的对边,若
中,a,b,c分别是角A,B,C的对边,若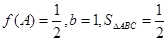 ,求a的值。
,求a的值。
已知函数
(I)求 的极小值;
的极小值;
(II)若 上为单调增函数,求m的取值范围;
上为单调增函数,求m的取值范围;
(III)设 (e是自然对数的底数)上至少存在一个
(e是自然对数的底数)上至少存在一个 成立,求m的取值范围。
成立,求m的取值范围。