(本小题满分12分)已知椭圆方程为 ,它的一个顶点为
,它的一个顶点为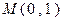 ,离心率
,离心率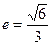 .(1)求椭圆的方程;(2)设直线
.(1)求椭圆的方程;(2)设直线 与椭圆交于A,B两点,坐标原点O到直线l的距离为
与椭圆交于A,B两点,坐标原点O到直线l的距离为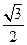 ,求△AOB面积的最大值.
,求△AOB面积的最大值.
选修4-5:不等式选讲
已知f(x)=x2-x+c,设x1,x2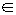 (0,1),且x1≠x2,求证:|f(x1)-f(x2)|<
(0,1),且x1≠x2,求证:|f(x1)-f(x2)|<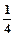 .
.
选修4—4:坐标系与参数方程
极坐标系中,求圆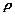 =
= 上的点到直线
上的点到直线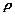 cos(
cos( =1的距离的取值范围.
=1的距离的取值范围.
选修4-1:几何证明选讲如图,在Rt⊿ABC中,AB=BC,以AB为直径的⊙O
交AC于D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:CE2=EF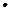 EA.
EA. 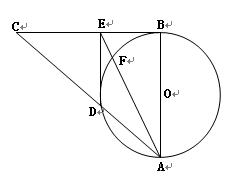
已知各项均为正数的数列{an}满足2a2n+1+3an+1an-2a2n=0(n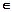
 )且a3+
)且a3+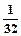 是a2,a4的等差中项,数列{bn}的前n项和Sn=n2
是a2,a4的等差中项,数列{bn}的前n项和Sn=n2
(1)求数列{an}与{bn}的通项公式;
(2)若Tn= ,求证:Tn<
,求证:Tn<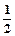
(3)若cn=-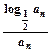 ,T/n=c1+c2+…+cn,求使T/n+n
,T/n=c1+c2+…+cn,求使T/n+n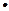 2n+1>125成立的正整数n的最小值
2n+1>125成立的正整数n的最小值
已知函数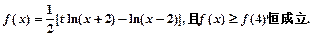
(1)求t的值;
(2)求x为何值时,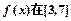 上取得最大值;
上取得最大值;
(3)设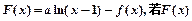 是单调递增函数,求a的取值范围.
是单调递增函数,求a的取值范围.