文(本小题满分12分)已知函数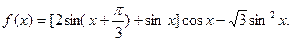
(I)若函数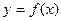 的图象关于直线
的图象关于直线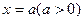 对称,求a的最小值;
对称,求a的最小值;
(II)若存在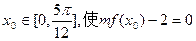 成立,求实数m的取值范围.
成立,求实数m的取值范围.
若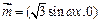 ,
,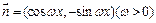 ,函数
,函数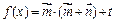 图象对称中心到对称轴最小距离为
图象对称中心到对称轴最小距离为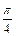 ,当
,当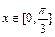 时f(x)的最大值为1.(1)求f(x)解析式;(2)若
时f(x)的最大值为1.(1)求f(x)解析式;(2)若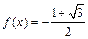 ,
,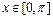 ,求x的值.
,求x的值.
(本小题满分12分)已知椭圆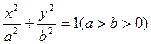 的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足

点P是线段F1Q与该椭圆的交点,
点T在线段F2Q上,并且满足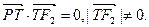
(Ⅰ)设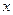 为点P的横坐标,证明
为点P的横坐标,证明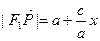 ;
;
(Ⅱ)求点T的轨迹C的方程;(Ⅲ)试问:在点T的轨迹C上,是否存在点M,
使△F1MF2的面积S= 若存在,求∠F1MF2的正切值;若不存在,请说明理由.
若存在,求∠F1MF2的正切值;若不存在,请说明理由.
(本小题满分12分)
一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数: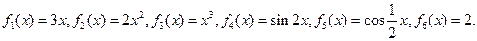
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是偶函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有奇函数的卡片则停止抽取,否则继续进行. 求抽取次数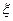 的分布列、数学期望和方差.
的分布列、数学期望和方差.
(本小题满分12分)
已知函数 R).(1)若
R).(1)若 在
在 时取得极值,求
时取得极值,求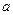 的值;
的值;
(2)求 的单调区间;(3)求证:当
的单调区间;(3)求证:当 时,
时, .
.