从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
(Ⅰ)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(Ⅱ)求频率分布直方图中的a,b的值;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为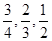 ,乙队每人答对的概率都是
,乙队每人答对的概率都是 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用 表示甲队总得分.
表示甲队总得分.
(I)求随机变量 的分布列及其数学期望E(
的分布列及其数学期望E( );
);
(Ⅱ)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率.
在△ABC中角,A,B,C所对的边分别为a,b,c,向量m=(cos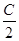 ,1),n=(一l,sin(A+B)),且m⊥n.
,1),n=(一l,sin(A+B)),且m⊥n.
( I)求角C的大小;
(Ⅱ)若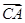 ·
· ,且a+b =4,求c.
,且a+b =4,求c.
已知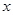 满足不等式
满足不等式 ,求函数
,求函数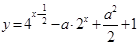 的最小值.
的最小值.
函数
 为奇函数,其图象在点
为奇函数,其图象在点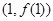 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数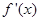 的最小值为
的最小值为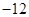 .
.
(1)求 ,
, ,
,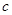 的值;
的值;
(2)求函数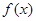 的单调递增区间,并求函数
的单调递增区间,并求函数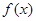 在
在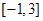 上的最大值和最小值.
上的最大值和最小值.
记关于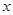 的不等式
的不等式 的解集为
的解集为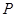 ,不等式
,不等式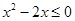 的解集为
的解集为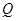 .
.
(1)若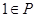 ,求实数
,求实数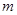 的取值范围;
的取值范围;
(2)若 ,求集合
,求集合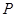 ;
;
(3)若 且
且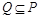 ,求实数
,求实数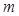 的取值范围.
的取值范围.