如图所示,劲度系数为k的轻弹簧,左端连着绝缘介质小球B，右端连在固定板上，放在光滑绝缘的水平面上。整个装置处在场强大小为E、方向水平向右的匀强电场中。现有一质量为m、带电荷量为+q的小球A，从距B球为S处自由释放，并与B球发生碰撞。碰撞中无机械能损失，且A球的电荷量始终不变。已知B球的质量M=3m，B球被碰后作周期性运动，其运动周期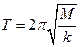
(A、B小球均可视为质点)。
(1)求A球与B球第一次碰撞后瞬间，A球的速度V1和B球的速度V2；
(2)要使A球与B球第二次仍在B球的初始位置迎面相碰，求劲度系数k的可能取值。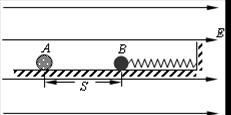
LC振荡电路中可变电容器电容C的取值范围为10 pF—360 pF，线圈的自感系数L="1.0" mH，求该振荡电路能获得的振荡电流的最高频率和最低频率各是多少.
已知在一个LC回路中，电容C="0.04" μF，电感L="6.0" mH，求这个电路的固有频率.
如图14-2-8所示LC回路中C是一平行板电容器，两板水平放置，开关断开时，电容器内带电灰尘恰好静止，当开关S闭合后，灰尘在电容器内运动，若C="4" μF， L="0.1" mH，求：
（1）从S闭合时开始计时，经过2π×10-5 s时，电容器内灰尘的加速度大小是多少？
（2）当灰尘的加速度多大时，线圈中电流最大？
图14-2-8
如图14-2-7所示电路，K先接通a触点，让电容器充电后再接通b触点，设这时可变电容器电容为C，线圈自感系数为L，
图14-2-7
（1）经过多长时间电容C上电荷第一次释放完？
（2）这段时间内电流如何变化？线圈两端电压如何变化？
（3）在振荡过程中将电容C变小，与振荡有关的物理量中哪些将随之改变？哪些将保持变化？
如图14-2-6所示，线圈的自感系数为3 μH，在线圈的中间有抽头2，电容器的电容可在300 pF—150 pF之间变化，S为转换开关。求此回路的最大周期和最大频率。
图14-2-6