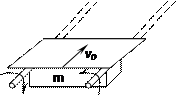
如图所示长为L质量为M的长木板静止在光滑水平面上,A,B为其端点,O为中心,质量为m长度可忽略的小木块以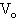 水平地沿木块表面滑来,两物体间动摩擦因数为μ,问
水平地沿木块表面滑来,两物体间动摩擦因数为μ,问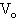 在什么范围内才能使小木块滑到OB之间停下来?
在什么范围内才能使小木块滑到OB之间停下来?
如图9所示,用F ="10" N的水平拉力,使质量m ="2.0" kg的物体由静止开始沿光滑水平面做匀加速直线运动. 求:
(1)物体加速度a的大小;
(2)物体在t=2.0 s内通过的距离.
如图所示,在磁感应强度B=0.2 T、方向与纸面垂直的匀强磁场中,有水平放置的两平行导轨ab、cd,其间距l=50 cm,a、c间接有电阻R.现有一电阻为r的导体棒MN跨放在两导轨间,并以v=10 m/s的恒定速度向右运动,a、c间电压为0.8 V,且a点电势高.其余电阻忽略不计.问:
⑴导体棒产生的感应电动势是多大?
⑵通过导体棒电流方向如何?磁场的方向是指向纸里,还是指向纸外?
⑶R与r的比值是多少?
如图一辆质量为500kg的汽车静止在一座半径为50m的圆弧形拱桥顶部.(取g=10m/s2)
(1)此时汽车对圆弧形拱桥的压力是多大?
(2)如果汽车以6m/s的速度经过拱桥的顶部,则汽车对圆弧形拱桥的压力是多大?
(3)汽车以多大速度通过拱桥的顶部时,汽车对圆弧形拱桥的压力恰好为零?
把一根长l = 10cm的导线垂直磁感线方向放入如图所示的匀强磁场中,
(1)当导线中通以I1 = 2A的电流时,导线受到的安培力大小为1.0×10-7N,则该磁场的磁感应强度为多少?
(2)若该导线中通以I2 = 3A的电流,则此时导线所受安培力大小是多少?方向如何?
如图14,如一质量m=20kg的钢件,架在两根完全相同的、平行的长直圆柱上,钢件的重心与两柱等距,两柱的轴线在同一水平面内,圆柱的半径r=0.025m,钢件与圆柱间的滑动摩擦系数μ=0.20,两圆柱各绕自己的轴线做转向相反的转动,角速度ω=40rad/s,若沿平行于柱轴方向施加力推着钢件做速度为v0=0.05m/s的匀速运动,推力是多大?设钢件左右受光滑槽限制(图中未画出),不发生横向运动