现有6本不同的书,如果(1)分成三组,一组3本,一组2本,一组1本;
(2)分给三个人,一人3本,一人2本,一人1本;
(3)平均分成三个组.
分别求分法种数.
(本小题满分10分)选修4-5:不等式选讲
已知函数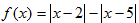
(1)若关于 的不等式
的不等式 有解,求
有解,求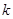 的最大值;
的最大值;
(2)求不等式: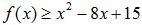 的解集.
的解集.
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线 (
(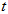 为参数),
为参数),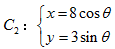 (
(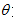 为参数).
为参数).
(1)化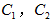 的方程为普通方程;
的方程为普通方程;
(2)若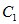 上的点对应的参数为
上的点对应的参数为 为
为 上的动点,求
上的动点,求 中点
中点 到直线
到直线 (
(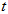 为参数)距离的最小值.
为参数)距离的最小值.
(本小题满分10分)选修4-1:几何证明选讲
已知在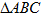 中,
中,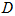 是
是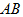 上一点,
上一点, 的外接圆交
的外接圆交 于
于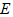 ,
, .
.
(1)求证: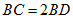 ;
;
(2)若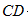 平分
平分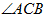 ,且
,且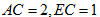 ,求
,求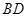 的长.
的长.
设函数 ,曲线
,曲线 过点P(1,0),且在P点处的切线的斜率为2,
过点P(1,0),且在P点处的切线的斜率为2,
(1)求 的值。
的值。
(2)证明:
(本小题满分12分)已知直线 与椭圆
与椭圆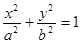
 相交于
相交于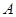 、
、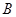 两点.
两点.
(1)若椭圆的离心率为 ,焦距为
,焦距为 ,求线段
,求线段 的长;
的长;
(2)若向量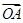 与向量
与向量 互相垂直(其中
互相垂直(其中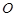 为坐标原点),当椭圆的离心率
为坐标原点),当椭圆的离心率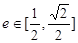 时,求椭圆长轴长的最大值.
时,求椭圆长轴长的最大值.