某商场为促销设计两套方案:(1)全场九折;(2)购物100元摸彩球打折,8个红色和8个绿色的玻璃球放在一个盒子里,顾客任意摸出8个球,仅有抽出的红球、绿球个数相等时不打折,两者相差一个时打9折,两者相差2个或2个以上时打8折,问商场应选择哪种方案更有利可图?
设函数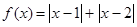 .
.
(1)画出函数y=f(x)的图像;
(2)若不等式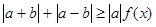 ,(a¹0,a、bÎR)恒成立,求实数x的范围.
,(a¹0,a、bÎR)恒成立,求实数x的范围.
(本小题满分10分)在直角坐标平面内,以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线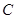 的极坐标方程是
的极坐标方程是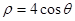 ,直线
,直线 的参数方程是
的参数方程是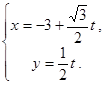 (
(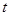 为参数)。
为参数)。
求极点在直线 上的射影点
上的射影点 的极坐标;
的极坐标;
若 、
、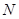 分别为曲线
分别为曲线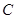 、直线
、直线 上的动点,求
上的动点,求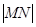 的最小值。
的最小值。
(本小题满分10分)从⊙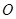 外一点
外一点 引圆的两条切线
引圆的两条切线 ,
, 及一条割线
及一条割线 ,
, 、
、 为切点.求证:
为切点.求证:
已知函数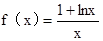
若函数在区间(a,a+ )上存在极值,其中a>0,求实数a的取值范围;
)上存在极值,其中a>0,求实数a的取值范围;
如果当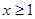 时,不等式
时,不等式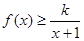 恒成立,求实数
恒成立,求实数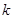 的取值范围。
的取值范围。
如图,椭圆C方程为 (
(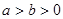 ),点
),点 为椭圆C的左、右顶点。
为椭圆C的左、右顶点。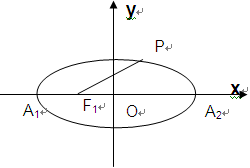
(1)若椭圆C上的点到焦点的距离的最大值为3,最小值为1,求椭圆的标准方程;
(2)若直线 与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足
与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足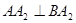 ,求证:直线
,求证:直线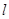 过定点,并求出该点的坐标。
过定点,并求出该点的坐标。