(本小题满分10分)从⊙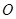 外一点
外一点 引圆的两条切线
引圆的两条切线 ,
, 及一条割线
及一条割线 ,
, 、
、 为切点.求证:
为切点.求证:
如图所示,动物园要建造一面靠墙的2间面积相同的矩形熊猫居室,如果可供建造围墙的材料总长是30m,那么宽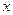 (单位:m)为多少才能使所建造的每间熊猫居室面积最大?每间熊猫居室的最大面积是多少?
(单位:m)为多少才能使所建造的每间熊猫居室面积最大?每间熊猫居室的最大面积是多少?
设曲线
(1)若函数 存在单调递减区间,求a的取值范围
存在单调递减区间,求a的取值范围
(2)若过曲线C外的点A(1,0)作曲线C的切线恰有三条,求a,b满足的关系式。
如图,斜率为1的直线 过抛物线
过抛物线 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。
(1)若|AB|=8,求抛物线 的方程;
的方程;
(2)设C为抛物线弧AB上的动点(不包括A,B两点),求 的面积S的最大值;
的面积S的最大值;
(3)设P是抛物线 上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
(本小题满分12分)
如图所示,平面PAD⊥平面ABCD,ABCD为正方形,PA⊥AD,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点。
(1)求证:BC//平面EFG;
(2)求三棱锥E—AFG的体积。
(本小题满分12分)
袋内装有6个球,每个球上都记有从1到6的一个号码,设号码为n的球重 克,这些球等可能地从袋里取出(不受重量、号码的影响)。
克,这些球等可能地从袋里取出(不受重量、号码的影响)。
(1)如果任意取出1球,求其重量大于号码数的概率;
(2)如果不放回地任意取出2球,求它们重量相等的概率。