设数列{an}前n项和为Sn,点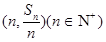 均在直线
均在直线 上.
上.
(1)求数列{an}的通项公式;
(2)设 ,Tn是数列{bn}的前n项和,试求Tn;
,Tn是数列{bn}的前n项和,试求Tn;
(3)设cn=anbn,Rn是数列{cn}的前n项和,试求Rn.
某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
但国家每天分配给该厂的煤、电有限, 每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?
设命题 实数
实数 满足
满足 ,其中
,其中 .命题
.命题 实数
实数 满足
满足 .
.
(1)若 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是 成立的必要不充分条件,求实数
成立的必要不充分条件,求实数 的取值范围.
的取值范围.
在 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, 且
且 .
.
(1)求 的面积;
的面积;
(2)若 ,求角
,求角 .
.
在平面直角坐标系xOy中,△ABC的顶点B、C的坐标为B(-2,0),C(2,0),直线AB,AC的斜率乘积为 ,设顶点A的轨迹为曲线E.
,设顶点A的轨迹为曲线E.
(1)求曲线E的方程;
(2)设曲线E与y轴负半轴的交点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与曲线E的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,试求 的取值范围.
的取值范围.