过抛物线y2=2px(p>0)上一定点P(x0,y0)(y0>0)作两条直线分别交抛物线于A(x1,y1)、B(x2,y2).
(1)求该抛物线上纵坐标为 的点到其焦点F的距离;
的点到其焦点F的距离;
(2)当PA与PB的斜率存在且倾斜角互补时,求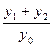 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.
用长为32米的篱笆围一个矩形养鸡场,设围成的矩形一边长为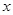 米,面积为
米,面积为 平方米.
平方米.
(1)求 关于
关于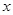 的函数关系式;
的函数关系式;
(2)当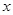 为何值时,围成的养鸡场面积为60平方米?
为何值时,围成的养鸡场面积为60平方米?
(3)能否围成面积为70平方米的养鸡场?如果能,求出其边长;如果不能,说明理由.
为了提高学生写好汉字的积极性,某校组织全校学生参加汉字听写比赛,比赛成绩从高到低只分A、B、C、D四个等级.若随机抽取该校部分学生的比赛成绩进行统计分析,并绘制了如下的统计图表: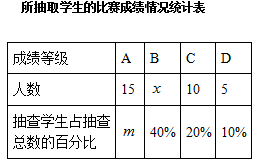
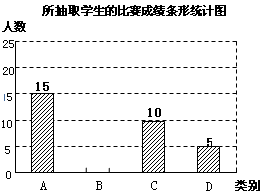
根据图表的信息,回答下列问题:
(1)本次抽查的学生共有 名;
(2)表中 和
和 所表示的数分别为:
所表示的数分别为: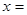 ,
,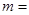 ,并在图中补全条形统计图;
,并在图中补全条形统计图;
(3)若该校共有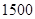 名学生,请你估计此次汉字听写比赛有多少名学生的成绩达到B级及B级以上?
名学生,请你估计此次汉字听写比赛有多少名学生的成绩达到B级及B级以上?
一辆客车从甲地出发前往乙地,平均速度 (千米/小时)与所用时间
(千米/小时)与所用时间 (小时)的函数关系如图所示,其中
(小时)的函数关系如图所示,其中 .
.
(1)直接写出 与
与 的函数关系式;
的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶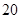 千米,
千米,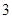 小时后两车相遇.
小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站 、
、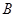 ,它们相距
,它们相距 千米,当客车进入
千米,当客车进入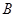 加油站时,货车恰好进入
加油站时,货车恰好进入 加油站(两车加油的时间忽略不计),求甲地与
加油站(两车加油的时间忽略不计),求甲地与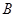 加油站的距离.
加油站的距离.
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AC的延长线相交于点F,且AC=8,tan∠BDC=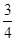 .求线段CF的长.
.求线段CF的长.
经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同.
(1)一辆正常行使的汽车经过某十字路口,则它向左转的概率为 ;
(2)现有甲、乙两辆汽车要经过这个十字路口,请用树形图或列表法表示出这两辆汽车行驶方向所有可能的结果,并求这两辆汽车都向左转的概率.