对于抛物线y2=2px(p>0),F为其焦点,过点F的直线l与抛物线交于A(x1,y1)、B(x2,y2)两点.
(1)求弦AB的长(用x1、x2、p表示);
(2)当AB⊥x轴时,求AB的长;
(3)判断以AB为直径的圆与抛物线的准线l的位置关系.
已知等差数列 的前
的前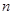 项和为
项和为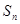 ,且
,且 ,
, ,在等比数列
,在等比数列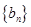 中,
中,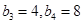 ,
,
(1)求 及
及 ;
;
(2)设数列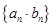 的前
的前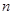 项和
项和 ,求
,求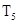
已知直线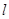

(1)若直线的斜率小于2,求实数 的取值范围;
的取值范围;
(2)若直线分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最大值及此时直线的方程.
将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷2次,将得到的点数分别记为a,b.
(1)求直线ax+by+5=0与圆x2+y2=1相切的概率;
(提示:点到直线的距离公式: )
)
(2)将a,b,5的值分别作为三条线段的长,求这三条线段围成等腰三角形的概率.
下面是计算应纳税所得额的算法过程,其算法如下:
第一步输入工资x(注x<=5000);
第二步如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x-800);
否则 y=25+0.1(x-1300)
第三步输出税款y, 结束.
请写出该算法的程序框图.
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?