如图,给出了一个三角形数阵,已知每一列的数成等差数列,从第3行起,每一行的数成等比数列,每一行的公比都相等.记第 行第
行第 列的数为
列的数为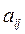 (
(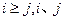 ∈N*).
∈N*).
(1)试写出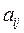 关于
关于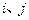 的表达式,并求
的表达式,并求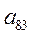 ;
;
(2)设数阵中第n行的所有数之和为An, 求An
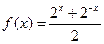
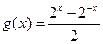
(1)计算: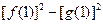 ;
;
(2)证明: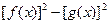 是定值
是定值
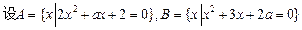
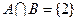
(1)求 的值及集合
的值及集合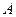 、
、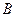 ;
;
(2)设全集 ,求
,求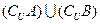 的所有子集
的所有子集
已知f(x)= [3ln(x+2)-ln(x-2)]
[3ln(x+2)-ln(x-2)]
(Ⅰ)求x为何值时,f(x)在[3,7]上取得最大值;
(Ⅱ)设F(x)=aln(x-1)-f(x),若F(x)是单调递增函数,求a的取值范围。
已知数列{an}的各项均是正数,其前n项和为sn,满足(p-1)sn=p2-an,其中p为正常数,且p≠1。
(Ⅰ)求数列{an}的通项公式:
(Ⅱ)设bn=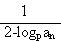 (n∈N※),数列{bnbn+2}的前n项和为Tn,求证:
(n∈N※),数列{bnbn+2}的前n项和为Tn,求证:
Tn<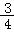
设A(x1,y1),B(x2,y2)是椭圆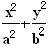 =1(a>b>0)上的两点,已知向量m(
=1(a>b>0)上的两点,已知向量m(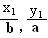 ) ,n(
) ,n(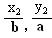 ),若m·n=0且椭圆的离心率e=
),若m·n=0且椭圆的离心率e=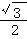 ,短轴长为2,O为坐标原点:
,短轴长为2,O为坐标原点:
(Ⅰ)求椭圆的方程:
(Ⅱ)若直线AB过椭圆的焦点F(0,c),(为半焦距),求直线AB的斜k率的值:
(Ⅲ)试问:△AOB的面积是否为定值?