为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用,经测量 AB=100m,BC=80m,AE=30m,AF=20m.
(1)求直线EF的方程.
(2)应如何设计才能使草坪的占地面积最大?
已知数列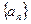 中,
中,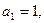 且点
且点 在直线
在直线 上.
上.
(1)求数列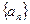 的通项公式;
的通项公式;
(2)若函数
求函数 的最小值;
的最小值;
(3)设 表示数列
表示数列 的前
的前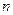 项和.试问:是否存在关于
项和.试问:是否存在关于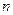 的整式
的整式 ,使得
,使得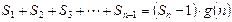 对于一切不小于2的自然数
对于一切不小于2的自然数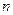 恒成立? 若存在,写出
恒成立? 若存在,写出 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
设斜率为 的直线
的直线 交椭圆
交椭圆 :
: 于
于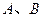 两点,点
两点,点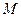 为弦
为弦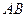 的中点,直线
的中点,直线 的斜率为
的斜率为 (其中
(其中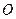 为坐标原点,假设
为坐标原点,假设 、
、 都存在).
都存在).
(1)求 ×
× 的值.
的值.
(2)把上述椭圆 一般化为
一般化为 (
(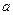 >
> >0),其它条件不变,试猜想
>0),其它条件不变,试猜想 与
与 关系(不需要证明).请你给出在双曲线
关系(不需要证明).请你给出在双曲线 (
(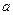 >0,
>0, >0)中相类似的结论,并证明你的结论.
>0)中相类似的结论,并证明你的结论.
有一种变压器铁芯的截面呈正十字形,为保证所需的磁通量,要求正十字形的面积为4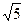 cm2,为了使用来绕铁芯的铜线最省,即正十字形外接圆周长最短,应如何设计 正十字形的长和宽?
cm2,为了使用来绕铁芯的铜线最省,即正十字形外接圆周长最短,应如何设计 正十字形的长和宽?
已知函数 是奇函数.
是奇函数.
(1)求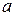 的值;
的值;
(2)判断函数 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)求函数的值域.
已知集合 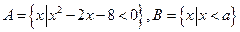 .
.
(1)若 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若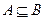 ,求实数
,求实数 的取值范围.
的取值范围.