某单位从市场上购进一辆新型轿车,购价为36万元,该单位使用轿车时,一年需养路费、保险费、汽油费、年检费等约需6万元,同时该车的年折旧率为10%(即这辆车每年减少它的价值的10%),试问:使用多少年后,该单位花费在该车上的费用就达36万元,并说明理由。
设函数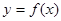 定义在
定义在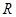 上,对于任意实数
上,对于任意实数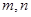 ,恒有
,恒有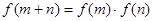 ,且当
,且当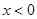 时,
时,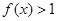
(1)求证: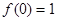 ,且当
,且当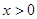 时,
时, 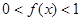
(2)求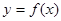 在
在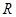 上的单调性.
上的单调性.
(3)设集合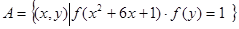 ,
,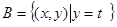 ,且
,且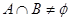 ,
,
求实数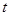 的取值范围.
的取值范围.
某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元;当用水超过4吨时,超过部分每吨3.00元。某月甲、乙两户共交水费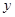 元,已知甲、乙两户该月用水量分别为
元,已知甲、乙两户该月用水量分别为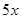 吨和
吨和 吨。
吨。
(1)求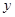 关于
关于 的函数;
的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费。
已知二次函数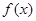 满足
满足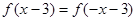 ,且该函数的图像与
,且该函数的图像与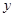 轴交于点
轴交于点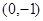 ,在
,在 轴上截得的线段长为
轴上截得的线段长为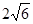 。
。
(1)确定该二次函数的解析式;
(2)当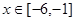 时,求
时,求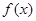 值域。
值域。
已知集合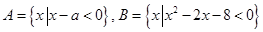 .
.
(1)若 ,全集
,全集 ,求
,求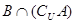 ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题11分)如图,三棱锥C—ABD,CB = CD,AB = AD,∠BAD = 90°。E、F分别是BC、AC的中点。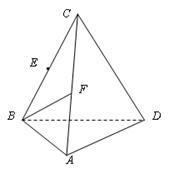
(1)求证:AC⊥BD;
(2)若CA = CB,求证:平面BCD⊥平面ABD
(3)在 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出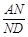 的值
的值