(本小题11分)如图,三棱锥C—ABD,CB = CD,AB = AD,∠BAD = 90°。E、F分别是BC、AC的中点。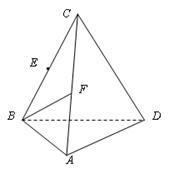
(1)求证:AC⊥BD;
(2)若CA = CB,求证:平面BCD⊥平面ABD
(3)在 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出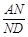 的值
的值
(本小题满分12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据完成以下2×2列联表,并运用独 立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
| 爱看课外书 |
不爱看课外书 |
总计 |
|
作文水平 好 好 |
|||
| 作文水平一般 |
|||
| 总计 |
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为1、2、3、4、5,某5名爱看课外书且作文水平一般的学生也 分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
参考公式: ,其中
,其中 .
.
参考数据:
 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分12分)
锐角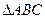 中,角A、B、
中,角A、B、 C所对的边分别为
C所对的边分别为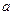 、
、 、
、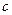 ,且
,且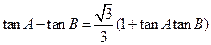 .
.
(Ⅰ)若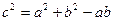 ,求角A、B、C大小;
,求角A、B、C大小;
(Ⅱ)已知向量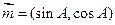 ,
,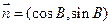 ,求
,求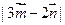 的取值范围.
的取值范围.
、选修4-5:不等式选讲
设函数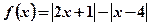 。(1)求不等式
。(1)求不等式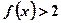 的解集;(2)求函数
的解集;(2)求函数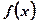 的最小值
的最小值
选修4-4:极坐标与参数方程
已知直线的极坐标方程为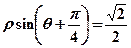 ,圆
,圆 的参数方程为
的参数方程为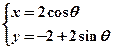 (其中
(其中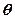 为参数)
为参数)
(1)将直线的极坐标方程化为直角坐标方程;(2)求圆 上的点到直线的距离的最小值
上的点到直线的距离的最小值
选修4-1:几何证明选讲
如图 内
内 接于圆
接于圆 ,
,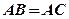 ,直线
,直线 切圆
切圆 于点
于点 ,弦
,弦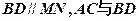 相交于点
相交于点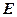 。(1)求证
。(1)求证 ≌
≌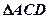 ;(2)若
;(2)若