设函数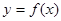 定义在
定义在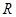 上,对于任意实数
上,对于任意实数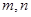 ,恒有
,恒有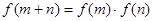 ,且当
,且当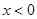 时,
时,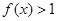
(1)求证: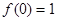 ,且当
,且当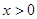 时,
时, 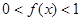
(2)求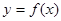 在
在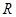 上的单调性.
上的单调性.
(3)设集合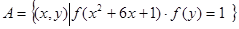 ,
,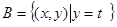 ,且
,且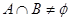 ,
,
求实数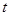 的取值范围.
的取值范围.
已知点M(-2,0),N(2,0),动点P满足条件|PM|-|PN|=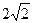 ,记动点P的轨迹为C.
,记动点P的轨迹为C.
(1)求C的方程;
(2)若A、B是曲线C上不同的两点,O是坐标原点,求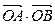 的最小值.
的最小值.
如图,已知中心在原点,焦点在x轴上的椭圆经过点(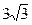 ,
, ),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.
),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.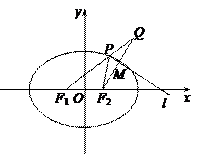
(1)求椭圆的标准方程;
(2)设P是椭圆上不同于左右顶点的动点,延长F1P至Q,使Q、F2关于∠F1PF2的外角平分线l对称,求F2Q与l的交点M的轨迹方程.
(1)设x∈R,比较x3与x2-x+1的大小.
(2)设a>0,b>0,求证: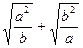 ≥
≥ .
.
已知圆M的半径为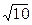 ,圆心在直线y=2x上,圆M被直线x-y=0截得的弦长为
,圆心在直线y=2x上,圆M被直线x-y=0截得的弦长为 ,求圆M的方程
,求圆M的方程
