如图，已知中心在原点，焦点在x轴上的椭圆经过点（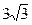
，
），且它的左焦点F1将长轴分成2∶1，F2是椭圆的右焦点．
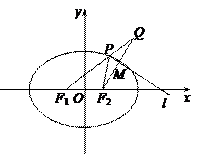
（1）求椭圆的标准方程；
（2）设P是椭圆上不同于左右顶点的动点，延长F1P至Q，使Q、F2关于∠F1PF2的外角平分线l对称，求F2Q与l的交点M的轨迹方程．
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截面得，已知FA⊥平面ABC，AB＝2，BD＝1，AF＝2， CE＝3，O为AB的中点．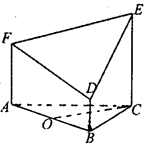
（1）求证：OC⊥DF；
（2）求平面DEF与平面ABC相交所成锐二面角的大小；
（3）求多面体ABC—FDE的体积V．
甲、乙、丙三人独立参加某企业的招聘考试，根据三人的专业知识、应试表现、工作经验等综合因素，三人被招聘的概率依次为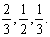
用
表示被招聘的人数。
（1）求三人中至少有一人被招聘的概率；
（2）求随机变量的分布列和数学期望。
已知函数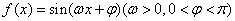
的一系列对应值如表：
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
|
 |
|
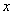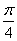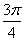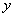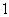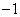（1）求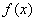
的解析式；
（2）若在
中，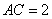
，
，
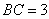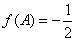（A为锐角），求的面积．
已知函数
，（
为实常数）
（1）若
，将
写出分段函数的形式，并画出简图，指出其单调递减区间；
（2）设在区间
上的最小值为
，求的表达式。
已知向量
，
且
，
函数
图象上相邻两条对称轴之间的距离是
，
（1）求
值；
（2）求函数的单调递减区间；
（3）设函数
，若
为偶函数，，求的最大值及
相应的
值