如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截面得,已知FA⊥平面ABC,AB=2,BD=1,AF=2, CE=3,O为AB的中点.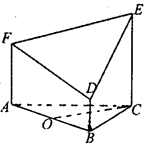
(1)求证:OC⊥DF;
(2)求平面DEF与平面ABC相交所成锐二面角的大小;
(3)求多面体ABC—FDE的体积V.
(1)已知函数f(x)=|x-1|+|x-a|.若不等式f(x)≥a恒成立,求实数a的取值范围.
(2).如图,圆O的直径为AB且BE为圆O的切线,点C为圆O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与圆O交于D,与BE交于E,连结BD、CD.
(Ⅰ)求证:∠DBE=∠DBC;
(Ⅱ)若HE=4,求ED.
已知函数f(x),如果存在给定的实数对 ,使得
,使得 恒成立,则称f(x)为“
恒成立,则称f(x)为“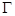 -函数”.
-函数”.
(1)判断函数 ,
,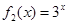 是否是“
是否是“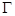 -函数”;
-函数”;
(2)若 是一个“
是一个“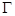 -函数”,求出所有满足条件的有序实数对(a,b);
-函数”,求出所有满足条件的有序实数对(a,b);
(3)若定义域为R的函数f(x)是“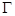 -函数”,且存在满足条件的有序实数对(0,1)和(1,4),当
-函数”,且存在满足条件的有序实数对(0,1)和(1,4),当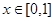 时,f(x)的值域为[1,2],求当
时,f(x)的值域为[1,2],求当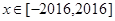 时函数f(x)的值域.
时函数f(x)的值域.
已知椭圆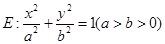 的离心率为
的离心率为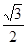 ,其长轴长与短轴长的和等于6.
,其长轴长与短轴长的和等于6.
(1)求椭圆E的方程;
(2)如图,设椭圆E的上.下顶点分别为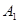 ,
, ,P是椭圆上异于
,P是椭圆上异于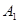 ,
, 的任意一点,直线
的任意一点,直线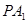 .
. 分别交x轴于点N.M,若直线OT与过点M.N的圆G相切,切点为T.证明:线段OT的长为定值.
分别交x轴于点N.M,若直线OT与过点M.N的圆G相切,切点为T.证明:线段OT的长为定值.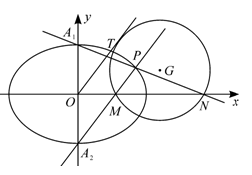
已知数列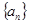 是递增的等比数列,满足
是递增的等比数列,满足 ,且
,且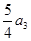 是
是 .
.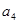 的等差中项,数列
的等差中项,数列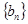 满足
满足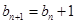 ,其前n项和为
,其前n项和为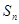 ,且
,且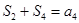 .
.
(1)求数列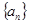 ,
,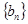 的通项公式;
的通项公式;
(2)数列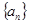 的前n项和为
的前n项和为 ,若不等式
,若不等式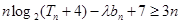 对一切
对一切 恒成立,求实数
恒成立,求实数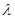 的取值范围.
的取值范围.
已知点A,B的坐标分别是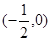 ,
, ,直线AM,BM相交于点M,且直线AM的斜率与直线BM的斜率的差是-1.
,直线AM,BM相交于点M,且直线AM的斜率与直线BM的斜率的差是-1.
(1)过点M的轨迹C的方程;
(2)过原点作两条互相垂直的直线 .
.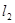 分别交曲线C于点A,C和B,D,求四边形ABCD面积的最小值.
分别交曲线C于点A,C和B,D,求四边形ABCD面积的最小值.