一投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分.经过多次试验,某人投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋。
(1)求该人在4次投掷中恰有三次投入红袋的概率;
(2)求该人两次投掷后得分 的数学期望
的数学期望 。
。
(本小题满分12分)已知向量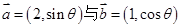 互相平行,其中
互相平行,其中 .
.
(1)求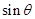 和
和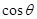 的值;
的值;
(2)若 ,求
,求 的值.
的值.
(本小题满分7分)选修4-5:不等式选讲
已知函数 .
.
(1)若不等式 的解集为
的解集为 ,求实数
,求实数 的值;
的值;
(2)若实数 ,
, ,
, 满足
满足 ,求
,求 的最大值.
的最大值.
(本小题满分7分)选修4-4:坐标系与参数方程
已知直线 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: .
.
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)判断直线 与圆
与圆 的位置关系.
的位置关系.
(本小题满分7分)选修4-2:矩阵与变换
已知矩阵 .
.
(1)矩阵 对应的变换把直线
对应的变换把直线
 变为直线
变为直线 ,求直线
,求直线 的方程;
的方程;
(2)求 的逆矩阵
的逆矩阵 .
.
(本小题满分14分)已知函数 (
( ).
).
(1)若 为函数
为函数 的极值点,求
的极值点,求 的值;
的值;
(2)若 ,
, 已知
已知
 ,
,
 ,若直线
,若直线 、
、 及直线
及直线 与函数
与函数 的图象所围成的封闭图形如阴影部分所示,求阴影面积
的图象所围成的封闭图形如阴影部分所示,求阴影面积 关于
关于 的函数
的函数 的最小值
的最小值 ;
; 证明不等式:
证明不等式: .
.