如图,四棱锥 中,底面
中,底面 是正方形,
是正方形, 是正方形
是正方形 的中心,
的中心,
 底面
底面 ,
, 是
是 的中点.
的中点.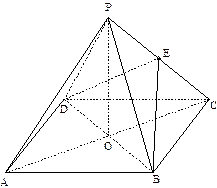
求证:(Ⅰ) ∥平面
∥平面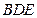 ;
;
(Ⅱ)平面
 平面
平面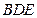 .
.
计算下列定积分
(1) |sinx|dx;(2)
|sinx|dx;(2) |x2-1|dx.
|x2-1|dx.
已知函数f(x)=(1+x)2-aln(1+x)2在(-2,-1)上是增函数,在(-∞,-2)上为减函数.
(1)求f(x)的表达式;
(2)若当x∈ 时,不等式f(x)<m恒成立,求实数m的值;
时,不等式f(x)<m恒成立,求实数m的值;
(3)是否存在实数b使得关于x的方程f(x)=x2+x+b在区间[0,2]上恰好有两个相异的实根,若存在,求实数b的取值范围.
已知函数f(x)=x3-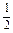 x2+bx+c.
x2+bx+c.
(1)若f(x)在(-∞,+∞)上是增函数,求b的取值范围;
(2)若f(x)在x=1处取得极值,且x∈[-1,2]时,f(x)<c2恒成立,求c的取值范围.
计算下列定积分
(1) x(x+1)dx;
x(x+1)dx;
(2)  (e2x+
(e2x+ )dx;
)dx;
(3)  sin2xdx.
sin2xdx.
已知函数f(x)= ,x∈[0,2].
,x∈[0,2].
(1)求f(x)的值域;
(2)设a≠0,函数g(x)= ax3-a2x,x∈[0,2].若对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0.求实数a的取值范围.
ax3-a2x,x∈[0,2].若对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0.求实数a的取值范围.