（本小题满分12分）
甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示只要面试合格就签约.乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约.设甲面试合格的概率为
，乙、丙面试合格的概率都是
，且面试是否合格互不影响．求：
（Ⅰ）至少有1人面试合格的概率；
（Ⅱ）签约人数
的分布列和数学期望．
（本小题满分12分）
如图，在四棱锥P-ABCD中，底面ABCD是矩形，M、N分别为PA、BC的中点， PD⊥平面ABCD，且PD=AD=
，CD=1.
（Ⅰ）证明：MN∥平面PCD；
（Ⅱ）证明：MC⊥BD；
（Ⅲ）求二面角A—PB—D的余弦值.
（本小题满分12分）
已知等比数列
中，
.
（Ⅰ）若
为等差数列，且满足
，求数列的通项公式；
（Ⅱ）若数列
满足
,求数列
的前
项和
.
必做题, 本小题10分．解答时应写出文字说明、证明过程或演算步骤．
在三棱锥ABCD中，平面DBC⊥平面ABC，△ABC为正三角形， AC=2，DC=DB=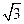
，
（1）求DC与AB所成角的余弦值；
（2）在平面ABD上求一点P，使得CP⊥平面AB D． 
必做题, 本小题10分．解答时应写出文字说明、证明过程或演算步骤．
某商场搞促销，当顾客购买商品的金额达到一定数量之后可以抽奖，根据顾客购买商品的金额，从箱中（装有4只红球，3只白球，且除颜色外，球的外部特征完全相同）每抽到一只红球奖励20元的商品（当顾客通过抽奖的方法确定了获奖商品后，即将小球全部放回箱中）
（1）当顾客购买金额超过500元而少于1000元（含1000元）时，可从箱中一次随机抽取3个小红球，求其中至少有一个红球的概率；
（2）当顾客购买金额超过1000元时，可一次随机抽取4个小球，设他所获奖商品的金额为
元，求的概率分布列和数学期望．
中，已知
，且
是1与
的等差中项.
；
，记数列
的前
项和为
，证明：