(本小题满分12分)
甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(Ⅰ)至少有1人面试合格的概率;
(Ⅱ)签约人数 的分布列和数学期望.
的分布列和数学期望.
(本小题满分14分)已知椭圆 :
: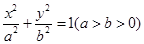 的上顶点为
的上顶点为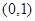 ,且离心率为
,且离心率为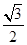 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)证明:过椭圆 :
: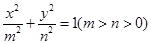 上一点
上一点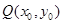 的切线方程为
的切线方程为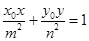 ;
;
(Ⅲ)从圆 上一点
上一点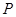 向椭圆
向椭圆 引两条切线,切点分别为
引两条切线,切点分别为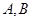 ,当直线
,当直线 分别与
分别与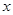 轴、
轴、 轴交于
轴交于 、
、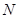 两点时,求
两点时,求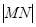 的最小值.
的最小值.
(本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB= ,PD⊥平面ABCD,PD=AD=1,点
,PD⊥平面ABCD,PD=AD=1,点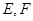 分别为AB和PD中点.
分别为AB和PD中点.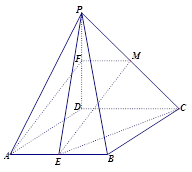
(Ⅰ)求证:直线AF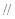 平面PEC ;
平面PEC ;
(Ⅱ)求PC与平面PAB所成角的正弦值.
(本小题满分12分)若定义在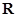 上的函数
上的函数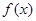 满足
满足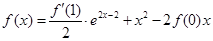 ,
,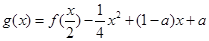 ,
,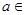 R.
R.
(Ⅰ)求函数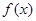 解析式;
解析式;
(Ⅱ)求函数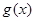 单调区间.
单调区间.
(本小题满分12分)已知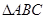 的三个角
的三个角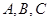 的对边分别为
的对边分别为 ,且
,且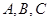 成等差数列,且
成等差数列,且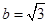 。数列
。数列 是等比数列,且首项
是等比数列,且首项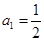 ,公比为
,公比为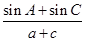 。
。
(1)求数列 的通项公式;
的通项公式;
(2)若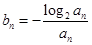 ,求数列
,求数列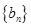 的前
的前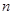 项和
项和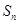 .
.
(本小题满分12分)已知函数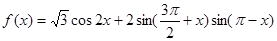 ,其中
,其中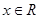 .
.
(Ⅰ)求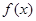 最小正周期及对称轴方程;
最小正周期及对称轴方程;
(Ⅱ)在锐角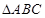 中,内角
中,内角 的对边分别为
的对边分别为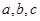 ,已知
,已知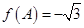 ,
,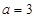 ,求
,求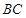 边上的高
边上的高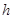 的最大值.
的最大值.