(本小题12分)设△ABC的内角A,B,C所对的边长分别为a,b,c,且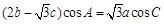 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若角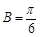 ,
,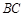 边上的中线
边上的中线 的长为
的长为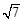 ,求
,求 的面积.
的面积.
(本大题满分18分)本大题共有3个小题,第1小题满分4分,第2小题满6分,第3小题满8分.
已知函数 ;
;
 ,
,
(1)当 为偶函数时,求
为偶函数时,求 的值。
的值。
(2)当 时,
时, 在
在 上是单调递增函数,求
上是单调递增函数,求 的取值范围。
的取值范围。
(3)当 时,(其中
时,(其中 ,
, ),若
),若 ,且函数
,且函数 的图像关于点
的图像关于点 对称,在
对称,在 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。
(本大题满分18分)本大题共有3个小题,第1小题满分4分,第2小题满6分,第3小题满8分.
已知集合 具有性质
具有性质 :对任意
:对任意 ,
, 与
与 至少一个属于
至少一个属于 .
.
(1)分别判断集合 与
与 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(2)①求证: ;
;
②求证: ;
;
(3)研究当 和
和 时,集合
时,集合 中的数列
中的数列 是否一定成等差数列.
是否一定成等差数列.
(本大题满分14分)
已知中心在原点,顶点A1、A2在x轴上,其渐近线方程是 ,双曲线过点
,双曲线过点
(1)求双曲线方程
(2)动直线 经过
经过 的重心G,与双曲线交于不同的两点M、N,问:是否存在直线
的重心G,与双曲线交于不同的两点M、N,问:是否存在直线 ,使G平分线段MN,证明你的结论
,使G平分线段MN,证明你的结论
本题共有2个小题,第1小题满分4分,第2小题满分8分.
已知 ,函数
,函数 .
.
(Ⅰ)当 时,求使
时,求使 成立的
成立的 的集合;
的集合;
(Ⅱ)求函数 在区间
在区间 上的最小值.
上的最小值.