下表是某小卖部5天卖出热茶的杯数与当天气温的对比表:
| 气温/℃ |
26 |
18 |
13 |
10 |
3 |
| 杯数 |
20 |
24 |
34 |
38 |
54 |
(1)请求出线性回归直线方程;
(2)如果某天的气温是-5℃时,预测这天小卖部卖出热茶的杯数。
(求线性回归方程系数公式 ,
,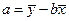 )
)
(本小题满 分10分)
分10分)
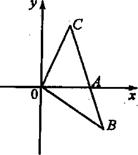
如图,在平面直角坐标系中 ,点
,点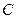 在第一象限内,
在第一象限内,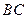 交
交 轴于点
轴于点 ,
, .
.
(1)求 的长;
的长;
(2)记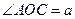 ,
,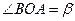 .(
.(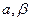 为锐角),求sina,sin
为锐角),求sina,sin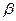 的值
的值
((本小题满分12分)
中心在原点,焦点在x轴上的椭圆,率心率 ,此椭圆与直线
,此椭圆与直线 交于A、B两点,且OA⊥OB(其中O为坐标原点).
交于A、B两点,且OA⊥OB(其中O为坐标原点).
(1)求椭圆方程;
(2)若M是椭圆上任意一点, 、
、 为椭圆的两个焦点,求
为椭圆的两个焦点,求 的取值范围;
的取值范围;
(
(本小题满分12分)
已知 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间 上是减函数,又
上是减函数,又
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若在区间 (m>0)上恒有
(m>0)上恒有 ≤x成立,求m的取值范围.
≤x成立,求m的取值范围.
(
(本小题满分12分)
已知数列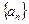 中,
中,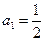 ,且当
,且当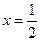 时,函数
时,函数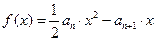 取得极值。
取得极值。
(Ⅰ)求数列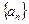 的通项公式;
的通项公式;
(Ⅱ)数列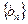 满足:
满足: ,
, ,证明:
,证明: 是等差数列,并求数列
是等差数列,并求数列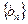 的通项公式通
的通项公式通 项及前
项及前 项和
项和 .
.
(
已知长方体ABCD-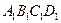 中,棱AB=BC=3,
中,棱AB=BC=3, =4,连结
=4,连结 , 在
, 在 上有点E,使得
上有点E,使得 ⊥平面EBD ,BE交
⊥平面EBD ,BE交 于F.
于F. 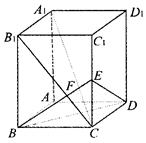
(1)求ED与平面 所成角的大小;
所成角的大小;
(2)求二面角E-BD-C的大小.