已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线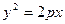 上,△ABC的重心与此抛物线的焦点F重合(如图)
上,△ABC的重心与此抛物线的焦点F重合(如图)
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标;
(3)求BC所在直线的方程. 
日常生活中,某些东西所含的热量比较高,对我们的身体有一定的影响,下表给出了不同类型八种饼干的数据,第一列数据表示八种饼干各含热量的百分比,第二列数据表示顾客对八种饼干所给予分数(百分制).
| 品种 |
所含热量的百分比 |
口味记录 |
| 1 |
25 |
89 |
| 2 |
34 |
89 |
| 3 |
20 |
80 |
| 4 |
19 |
78 |
| 5 |
26 |
75 |
| 6 |
20 |
71 |
| 7 |
19 |
65 |
| 8 |
24 |
62 |
(1)作出这些数据的散点图;
(2)求出回归直线;
(3)关于两个变量之间的关系,你能得出什么结论?
(4)为什么人们更喜欢吃位于回归直线上方的饼干而不是下方的饼干?
判断下列关系是否为相关关系:
(1)历史上,有人认为人们的着装与经济好坏有关系,着装越鲜艳,经济越景气,你认为着装与经济真的有这种相关关系吗?
(2)下面是6位同学的身高与体重的数据表:
| 身高(cm) |
168 |
173 |
176 |
179 |
181 |
185 |
| 体重(kg) |
56 |
59 |
60 |
65 |
64 |
68 |
画出散点图,并判断它们是否有相关关系.
从全校参加期末考试的试卷中,抽取一个样本,考察成绩(均为整数)的分布,将样本分成5组,绘成频率分布直方图,如图2-2-8中从左到右各小组的小矩形的高之比为2∶3∶6∶4∶1,最左边的一组频数是6.
图2-2-8
(1)求样本容量;
(2)求105.5~120.5这一组的频数及频率;
(3)如果成绩大于120分为优秀,估计这次考试成绩的优秀率.
求下列各组数据的方差与标准差(结果保留到小数点后一位):
(1)1,2,3,4,5,6,7,8,9;
(2)11,12,13,14,15,16,17,18,19;
(3)10,20,30,40,50,60,70,80,90.
并分析由这些结果可得出什么一般性结论.
已知数列 满足:
满足: ,且存在大于1的整数k使
,且存在大于1的整数k使 。
。
(1)用 表示m(不必化简)
表示m(不必化简)
(2)用k表示m(化成最简形式)
(3)若m是正整数,求k与m的值;