一个几何体的三视图如下图所示,其中主视图与左视图是腰长为6的等腰直角三角形,俯视图是正方形。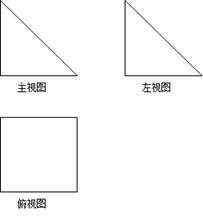
(Ⅰ)请画出该几何体的直观图,并求出它的体积;
(Ⅱ)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1? 如何组拼?试证明你的结论;
(Ⅲ)在(Ⅱ)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值.
(本小题满分12分)
在 中,角A,B,C所对的边分别为a,b,c, 若向量
中,角A,B,C所对的边分别为a,b,c, 若向量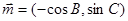 ,
, ,
,
且 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若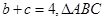 的面积
的面积 ,求
,求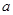 的值.
的值.
(本小题满分12分)已知命题 :不等式
:不等式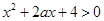 对一切
对一切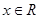 恒成立;命题
恒成立;命题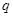 :函数
:函数 是增函数.若
是增函数.若 或
或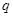 为真,
为真, 且
且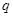 为假,求实数
为假,求实数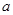 的取值范围.
的取值范围.
(本小题满分14分)已知函数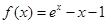 ,
,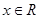 , 其中,
, 其中,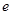 是自然对数的底数.函数
是自然对数的底数.函数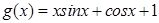 ,
,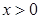 .
.
(Ⅰ)求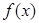 的最小值;
的最小值;
(Ⅱ)将 的全部零点按照从小到大的顺序排成数列
的全部零点按照从小到大的顺序排成数列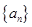 ,求证:
,求证:
(1)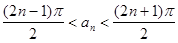 ,其中
,其中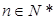 ;
;
(2)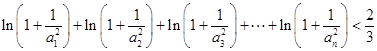 .
.
(本小题满分13分)如图,已知抛物线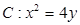 ,过焦点F任作一条直线与
,过焦点F任作一条直线与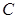 相交于
相交于 两点,过点
两点,过点 作
作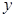 轴的平行线与直线
轴的平行线与直线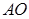 相交于点
相交于点 (
( 为坐标原点).
为坐标原点).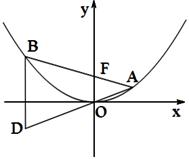
(Ⅰ)证明:动点 在定直线上;
在定直线上;
(Ⅱ)点P为抛物线C上的动点,直线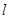 为抛物线C在P点处的切线,求点Q(0,4)到直线
为抛物线C在P点处的切线,求点Q(0,4)到直线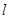 距离的最小值.
距离的最小值.
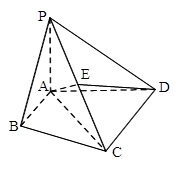
(本小题满分13分)在四棱锥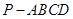 中,
中,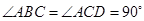 ,
,
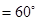 ,
,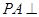 平面
平面 ,直线PC与平面ABCD所成角为
,直线PC与平面ABCD所成角为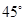 ,
,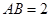 .
.
(Ⅰ)求四棱锥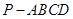 的体积
的体积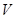 ;
;
(Ⅱ)若 为
为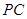 的中点,求证:平面
的中点,求证:平面
 平面
平面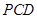 .
.