甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个2×2的列联表;
(2)试判断能否有99.5%的把握认为“考试成绩与班级有关”?参考公式:K2=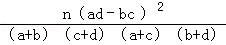 ;n=a+b+c+d
;n=a+b+c+d
| P(K2>k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
对于函数 ,若
,若 =x,则称x为
=x,则称x为 的“不动点”;若
的“不动点”;若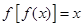 ,则称x为
,则称x为 “稳定点”,函数
“稳定点”,函数 的“不动点”和“稳定点”的集合分别记为A和B,既
的“不动点”和“稳定点”的集合分别记为A和B,既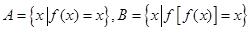 .
.
(1)证明:A B
B
(2)若
 ,且
,且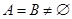 ,求实数a的取值范围.
,求实数a的取值范围.
解关于x不等式(x2-2)3-x3+2x2-2x-4>0
在三角形ABC中,证明余弦定理的正弦形式
已知函数 是定义在
是定义在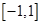 上的奇函数,若对于任意
上的奇函数,若对于任意 ,都有
,都有 且
且 >0时,有
>0时,有 >0
>0
(1)证明: 在
在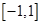 上为单调递增函数;
上为单调递增函数;
(2)解不等式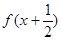 <
< ;
;