对于函数 ,若
,若 =x,则称x为
=x,则称x为 的“不动点”;若
的“不动点”;若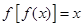 ,则称x为
,则称x为 “稳定点”,函数
“稳定点”,函数 的“不动点”和“稳定点”的集合分别记为A和B,既
的“不动点”和“稳定点”的集合分别记为A和B,既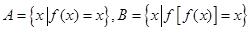 .
.
(1)证明:A B
B
(2)若
 ,且
,且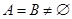 ,求实数a的取值范围.
,求实数a的取值范围.
用总长为14.8米的钢条制成一个长方体容器的框架,如果所制的容器的底面的长比宽多0.5米,那么高为多少时容器的容器最大?并求出它的最大容积.
已知函数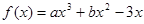 在
在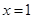 处取得极值-2.
处取得极值-2.
(1)求函数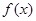 的解析式;
的解析式;
(2)求曲线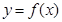 在点
在点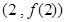 处的切线方程.
处的切线方程.
若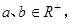 求证:
求证: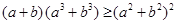 .
.
设抛物线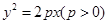 的焦点为
的焦点为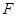 ,点
,点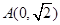 ,线段
,线段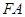 的中点在抛物线上.设动直线
的中点在抛物线上.设动直线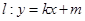 与抛物线相切于点
与抛物线相切于点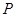 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点 ,以
,以 为直径的圆记为圆
为直径的圆记为圆 .
.
(1)求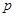 的值;
的值;
(2)证明:圆 与
与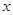 轴必有公共点;
轴必有公共点;
(3)在坐标平面上是否存在定点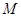 ,使得圆
,使得圆 恒过点
恒过点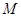 ?若存在,求出
?若存在,求出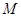 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
已知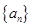 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项 ,
,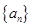 的部分项
的部分项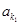 、
、 、…、
、…、 恰为等比数列,且
恰为等比数列,且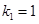 ,
,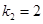 ,
,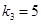 .
.
(1)求数列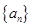 的通项公式
的通项公式 (用
(用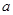 表示);
表示);
(2)若数列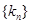 的前
的前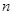 项和为
项和为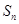 ,求
,求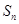 .
.