已知A、B、C是直线l上的三点,且|AB|=|BC|=6,⊙O′切直线l于点A,又过B、C作⊙O′异于l的两切线,设这两切线交于点P,求点P的轨迹方程.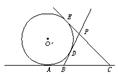
(本小题满分14分)如图4,已知 中,
中, ,
, ,
, ⊥
⊥
平面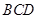 ,
,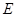 、
、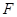 分别是
分别是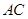 、
、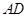 的中点.
的中点.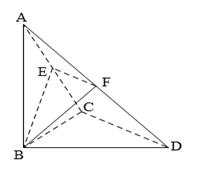
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)求四棱锥B-CDFE的体积V;
(3)求平面 与平面
与平面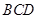 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(本小题满分12分)下图是某市今年1月份前30天空气质量指数(AQI)的趋势图.
(1)根据该图数据在答题卷中完成频率分布表,并在图中作出这些数据的频率分布直方图;

(图中纵坐标1/300即 ,以此类推)
,以此类推)
(2)当空气质量指数(AQI)小于100时,表示空气质量优良.某人随机选择当月1日至10日中的某一
天到达该市,并停留2天,设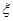 是此人停留期间空气质量优良的天数,求
是此人停留期间空气质量优良的天数,求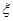 的数学期望.
的数学期望.
(本小题满分12分)已知函数 的最小正周期为
的最小正周期为 .
.
(1)求 的值;
的值;
(2)若 ,
, ,求
,求 的值.
的值.
(本小题满分13分)设 ,函数
,函数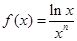 ,函数
,函数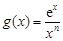 ,
, .
.
(Ⅰ)判断函数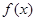 在区间
在区间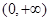 上是否为单调函数,并说明理由;
上是否为单调函数,并说明理由;
(Ⅱ)若当 时,对任意的
时,对任意的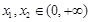 , 都有
, 都有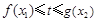 成立,求实数
成立,求实数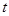 的取值范围;
的取值范围;
(Ⅲ)当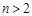 时,若存在直线
时,若存在直线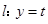 (
( ),使得曲线
),使得曲线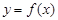 与曲线
与曲线 分别位于直线
分别位于直线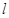 的两侧,写出
的两侧,写出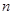 的所有可能取值. (只需写出结论)
的所有可能取值. (只需写出结论)
(本小题满分14分)设点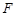 为椭圆
为椭圆 的右焦点,点
的右焦点,点 在椭圆
在椭圆 上,已知椭圆
上,已知椭圆 的离心率为
的离心率为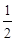 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设过右焦点 的直线
的直线 与椭圆相交于
与椭圆相交于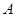 ,
, 两点,记
两点,记 三条边所在直线的斜率的乘积为
三条边所在直线的斜率的乘积为 ,求
,求 的最大值.
的最大值.