(本小题满分13分) 设 ,函数
,函数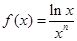 ,函数
,函数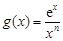 ,
, .
.
(Ⅰ)判断函数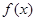 在区间
在区间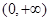 上是否为单调函数,并说明理由;
上是否为单调函数,并说明理由;
(Ⅱ)若当 时,对任意的
时,对任意的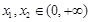 , 都有
, 都有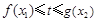 成立,求实数
成立,求实数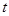 的取值范围;
的取值范围;
(Ⅲ)当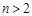 时,若存在直线
时,若存在直线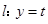 (
( ),使得曲线
),使得曲线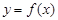 与曲线
与曲线 分别位于直线
分别位于直线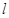 的两侧,写出
的两侧,写出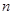 的所有可能取值. (只需写出结论)
的所有可能取值. (只需写出结论)
如图所示,已知 矩形ABCD所在平面,M、N分别是AB、PC的中点。
矩形ABCD所在平面,M、N分别是AB、PC的中点。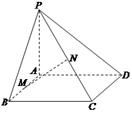
(1)求证: 平面PAD;
平面PAD;
(2)求证: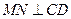
设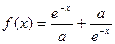 是定义在R上的函数
是定义在R上的函数
(1)f(x)可能是奇函数吗?
(2)当a=1时,试研究f(x)的单调性
已知△ABC的三个顶点分别为A(2,3),B(-1,-2),C(-3,4),求
(1)BC边上的中线AD所在的直线方程;
(2)△ABC的面积
某电厂冷却塔外形是如图所示的双曲线的一部分绕其中轴(双曲线的虚轴)旋转所成的曲面,其中A,A′是双曲线的顶点,C,C′是冷却塔上口直径的两个端点,B,B′是冷却塔下底直径的两个端点,已知AA′="14" m,CC′="18" m,BB′="22" m,塔高20 m.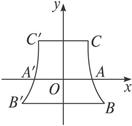
(1)建立坐标系并写出该曲线的方程;
(2)求冷却塔的容积(精确到10 m3,塔壁厚度不计,π取3.14)
直角梯形ABCD中∠DAB=90°,AD∥BC,AB=2,AD= ,BC=
,BC= .椭圆C以A、B为焦点且经过点D.
.椭圆C以A、B为焦点且经过点D.
(1)建立适当坐标系,求椭圆C的方程;
(2)若点E满足

 ,问是否存在不平行AB的直线l与椭圆C交于M、N两点且
,问是否存在不平行AB的直线l与椭圆C交于M、N两点且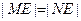 ,若存在,求出直线l与AB夹角的范围,若不存在,说明理由
,若存在,求出直线l与AB夹角的范围,若不存在,说明理由