某研究机构为了研究人的脚的大小(码)与身高(厘米)之间的关系,随机抽测了20人,得到如下数据:
| 序号 |
身高x |
脚长y |
序号 |
身高x |
脚长y |
| 1 |
176 |
42 |
11 |
179 |
44 |
| 2 |
175 |
44 |
12 |
169 |
43 |
| 3 |
174 |
41 |
13 |
185 |
45 |
| 4 |
180 |
44 |
14 |
166 |
40 |
| 5 |
170 |
42 |
15 |
174 |
42 |
| 6 |
178 |
43 |
16 |
167 |
42 |
| 7 |
173 |
42 |
17 |
173 |
41 |
| 8 |
168 |
40 |
18 |
174 |
42 |
| 9 |
190 |
46 |
19 |
172 |
42 |
| 10 |
171 |
42 |
20 |
175 |
41 |
(1)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”,“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成如下2×2列联表;
| |
高个 |
非高个 |
合计 |
| 大脚 |
|
|
|
| 非大脚 |
|
12 |
|
| 合计 |
|
|
20 |
(2)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为脚的大小与身高有关系? 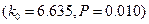
已知命题 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线。命题
轴上的双曲线。命题 曲线
曲线 与
与 轴交于不同的两点,若
轴交于不同的两点,若 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围。
的取值范围。
已知函数f(x)=- x3+
x3+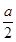 x2-2x(a∈R).
x2-2x(a∈R).
(1)当a=3时,求函数f(x)的单调区间;
(2)若对于任意x∈[1,+∞)都有f′(x)<2(a-1)成立,求实数a的取值范围;
(3)若过点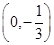 可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
如图,E是以AB为直径的半圆上异于点A、B的点,矩形ABCD所在的平面垂直于该半圆所在的平面,且AB=2AD=2
(1)求证: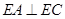
(2)设平面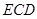 与半圆弧的另一个交点为
与半圆弧的另一个交点为
①试证: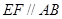
②若 求三棱锥
求三棱锥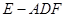 的体积
的体积
已知命题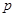 :方程
:方程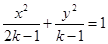 表示椭圆;
表示椭圆; :方程
:方程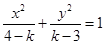 表示双曲线. 若“
表示双曲线. 若“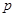 或
或 ”为真,“
”为真,“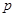 且
且 ” 为假,求实数
” 为假,求实数 的取值范围.
的取值范围.
如图, 中
中 ,平面
,平面 外一条线段AB满足AB∥DE,AB
外一条线段AB满足AB∥DE,AB ,AB⊥AC,F是CD的中点.
,AB⊥AC,F是CD的中点.
(1)求证:AF∥平面BCE
(2)若AC=AD,证明:AF⊥平面