在直角坐标系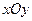 中,点P到两点
中,点P到两点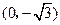 ,
, 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为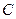 ,直线
,直线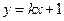 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若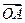
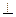
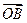 ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有|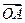 |>|
|>|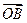 |
|
(本题8分)已 知函数
知函数
(1) 求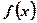 的定义域;
的定义域;
(2) 证明函数 在
在  上是减函数.
上是减函数.
(本题6分)设全集为R, ,
, ,求
,求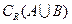 及
及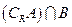
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求二面角A1-BP-E的大小。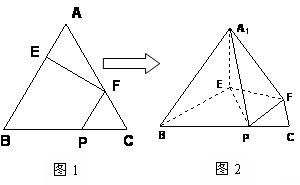
如图,A1A是圆柱的母线,AB是圆柱底面圆的直径, C是底面圆周上异于A,B的任意一点,A1A= AB=2.
(Ⅰ)求证: BC⊥平面A1AC;
(Ⅱ)求三棱锥A1-ABC的体积的最大值.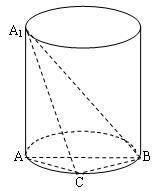
如图,在四棱锥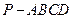 中,底面为直角梯形,
中,底面为直角梯形,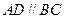 ,
,
 ,
, 底面
底面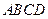 ,且
,且 ,
, 分别为
分别为 、
、 的中点。
的中点。
(Ⅰ)求证: ;
;
(Ⅱ)求 与平面
与平面 所成角的正弦值。
所成角的正弦值。