如图,已知:射线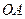 为
为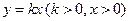 ,射线
,射线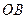 为
为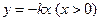 ,动点
,动点 在
在 的内部,
的内部,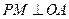 于
于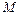 ,
,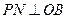 于
于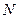 ,四边形
,四边形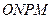 的面积恰为
的面积恰为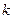 .
.
(1)当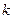 为定值时,动点
为定值时,动点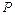 的纵坐标
的纵坐标 是横坐标
是横坐标 的函数,求这个函数
的函数,求这个函数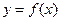 的解析式;
的解析式;
(2)根据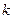 的取值范围,确定
的取值范围,确定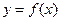 的定义域.
的定义域.
 |
如图,椭圆 :
: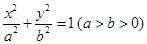 的右焦点为
的右焦点为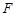 ,右顶点、上顶点分别为点
,右顶点、上顶点分别为点 、
、 ,且
,且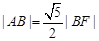 .
.
(1)求椭圆 的离心率;
的离心率;
(2)若斜率为2的直线 过点
过点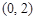 ,且
,且 交椭圆
交椭圆 于
于 、
、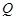 两点,
两点, .求直线
.求直线 的方程及椭圆
的方程及椭圆 的方程.
的方程.
为选拔选手参加“中国汉字听写大会”,某中学举行了一次“汉字听写大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为 )进行统计.按照
)进行统计.按照 ,
,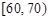 ,
, ,
, ,
,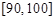 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在 ,
,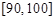 的数据).
的数据).
(1)求样本容量 和频率分布直方图中的
和频率分布直方图中的 、
、 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国汉字听写大会”,求所抽取的2名学生中至少有一人得分在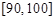 内的概率.
内的概率.
如图,设四棱锥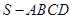 的底面为菱形,且∠
的底面为菱形,且∠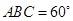 ,
, ,
, 。
。
(1)求证:平面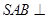 平面
平面 ;
;
(2)设 为
为 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积.
(本小题满分12分)已知 是正项数列,
是正项数列, ,且点
,且点 (
( )在函数
)在函数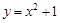 的图像上.
的图像上.
(1)求数列 的通项公式;
的通项公式;
(2)若列数 满足
满足 ,
,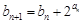 ,求证:
,求证: .
.
(本小题满分10分)选修4—5:不等式选讲
已知函数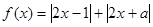 ,
, .
.
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)设 ,且当
,且当 时,
时, ,求
,求 的取值范围.
的取值范围.