设函数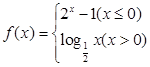 ,如果
,如果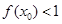 ,求
,求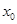 的取值范围.
的取值范围.
已知平面内两点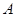 (-1,1),
(-1,1),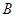 (1,3).
(1,3).
(Ⅰ)求过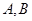 两点的直线方程;
两点的直线方程;
(Ⅱ)求过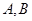 两点且圆心在
两点且圆心在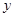 轴上的圆的方程.
轴上的圆的方程.
已知 是椭圆E:
是椭圆E: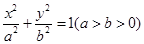 的两个焦点,抛物线
的两个焦点,抛物线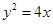 的焦点为椭圆E的一个焦点,直线y=
的焦点为椭圆E的一个焦点,直线y= 上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
(Ⅰ)求椭圆E的方程;
(Ⅱ)如图,过点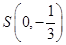 的动直线
的动直线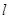 交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由。
交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由。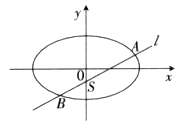
已知P(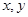 )为函数
)为函数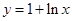 图像上一点,O为坐标原点,记直线OP的斜率
图像上一点,O为坐标原点,记直线OP的斜率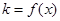 。
。
(Ⅰ)求函数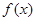 的单调区间;
的单调区间;
(Ⅱ)设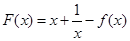 ,求函数
,求函数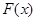 的最小值。
的最小值。
正项数列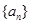 的前n项和为
的前n项和为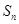 ,且
,且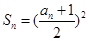 。
。
(Ⅰ)证明数列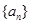 为等差数列并求其通项公式;
为等差数列并求其通项公式;
(2)设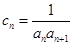 ,数列
,数列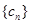 的前n项和为
的前n项和为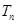 ,证明:
,证明: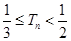 。
。