已知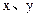 之间满足
之间满足
(1)方程 表示的曲线经过一点
表示的曲线经过一点 ,求b的值
,求b的值
(2)动点(x,y)在曲线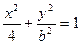 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值;
(3)由 能否确定一个函数关系式
能否确定一个函数关系式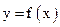 ,如能,求解析式;如不能,再加什么条件就可使
,如能,求解析式;如不能,再加什么条件就可使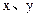 之间建立函数关系,并求出解析式。
之间建立函数关系,并求出解析式。
(
设直线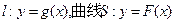 . 若直线l与曲线S同时满足下列两个条件:
. 若直线l与曲线S同时满足下列两个条件:
①直线l与曲线S相切且至少有两个切点;
②对任意x∈R都有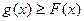 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
(1) 类比“上夹线”的定义,给出“下夹线”的定义;
(2) 已知函数 取得极小值
取得极小值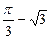 ,求a,b的值;
,求a,b的值;
(3) 证明:直线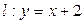 是(2)中曲线
是(2)中曲线 的“上夹线”。
的“上夹线”。
某养殖厂规定:饲料用完的第二天方可购买饲料,并且每批饲料可供n(n∈Z*)天使用.已知该厂每天需要饲料200公斤,每公斤饲料的价格为1.8元,饲料的保管费为平均每公斤每天0.03元(当天用掉的饲料不计保管费用),购买饲料每次支付运费300元.
(1)求该厂多少天购买一次饲料才能使平均每天支付的总费用最小;
(2)若提供饲料的公司规定,当一次购买饲料不少5吨时其价格可享受八五折优惠(即原价的85%).问该厂是否考虑利用此优惠条件,请说明理由.
已知
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)求函数 在
在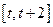
 上的最小值;
上的最小值;
(Ⅲ)对一切的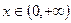 ,
, 恒成立,求实数
恒成立,求实数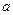 的取值范围.
的取值范围.
已知函数 单调递减,
单调递减,
(I)求a的值;
(II)是否存在实数b,使得函数 的图象恰有3个交点,若
的图象恰有3个交点,若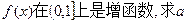 的取值范围数b的值;若不存在,试说明理由。
的取值范围数b的值;若不存在,试说明理由。
设函数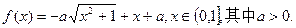
(1)若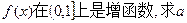 的取值范围;
的取值范围;
(2)求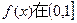 上的最大值.
上的最大值.