设直线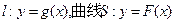 . 若直线l与曲线S同时满足下列两个条件:
. 若直线l与曲线S同时满足下列两个条件:
①直线l与曲线S相切且至少有两个切点;
②对任意x∈R都有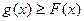 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
(1) 类比“上夹线”的定义,给出“下夹线”的定义;
(2) 已知函数 取得极小值
取得极小值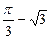 ,求a,b的值;
,求a,b的值;
(3) 证明:直线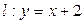 是(2)中曲线
是(2)中曲线 的“上夹线”。
的“上夹线”。
如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.
如图,△ 中,
中, ,
, ,
,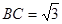 ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心 在边
在边 上,半圆与
上,半圆与 、
、 分别相切于点
分别相切于点 、
、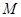 ,与
,与 交于点
交于点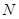 ),将△
),将△ 绕直线
绕直线 旋转一周得到一个旋转体.
旋转一周得到一个旋转体.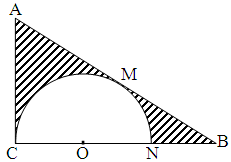
(1)求该几何体中间一个空心球的表面积的大小;
(2)求图中阴影部分绕直线 旋转一周所得旋转体的体积.
旋转一周所得旋转体的体积.
已知函数 的定义域为A,
的定义域为A,
(1)求A;
(2)若 ,且A∩B≠∅,求实数k的取值范围.
,且A∩B≠∅,求实数k的取值范围.
设函数 是定义在
是定义在 上的函数,并且满足下面三个条件:(1)对任意正数
上的函数,并且满足下面三个条件:(1)对任意正数 ,都有
,都有 ;(2)当
;(2)当 时,
时, ;(3)
;(3) ,
,
(Ⅰ)求 、
、 的值;
的值;
(Ⅱ)若不等式 成立,求
成立,求 的取值范围.
的取值范围.
(Ⅲ)若存在正数 ,使得不等式
,使得不等式 有解,求正数
有解,求正数 的取值范围.
的取值范围.
圆心在直线 上的圆
上的圆 经过点
经过点 ;
;
(Ⅰ)若过点 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)在 轴上是否存在定点
轴上是否存在定点 ,使得圆
,使得圆 上任意一点
上任意一点 到点
到点 (
( 为坐标原点)的距离与到点
为坐标原点)的距离与到点 的距离之比为常数,如果存在,求出点
的距离之比为常数,如果存在,求出点 的坐标并求出这个常数;如果不存在请说明理由.
的坐标并求出这个常数;如果不存在请说明理由.