设函数 是定义在
是定义在 上的函数,并且满足下面三个条件:(1)对任意正数
上的函数,并且满足下面三个条件:(1)对任意正数 ,都有
,都有 ;(2)当
;(2)当 时,
时, ;(3)
;(3) ,
,
(Ⅰ)求 、
、 的值;
的值;
(Ⅱ)若不等式 成立,求
成立,求 的取值范围.
的取值范围.
(Ⅲ)若存在正数 ,使得不等式
,使得不等式 有解,求正数
有解,求正数 的取值范围.
的取值范围.
根据如图所示的流程图,将输出的 的值依次分别记为
的值依次分别记为 ,将输出的
,将输出的 的值依次分别记为
的值依次分别记为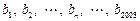 .
.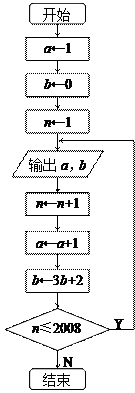
(Ⅰ)求数列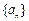 ,
, 通项公式;
通项公式;
(Ⅱ)依次在 与
与 中插入
中插入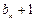 个3,就能得到一个新数列
个3,就能得到一个新数列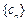 ,则
,则 是数列
是数列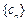 中的第几项?
中的第几项?
(Ⅲ)设数列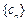 的前
的前 项和为
项和为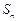 ,问是否存在这样的正整数
,问是否存在这样的正整数 ,使数列
,使数列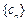 的前
的前 项的和
项的和 ,如果存在,求出
,如果存在,求出 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
设不等式组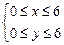 表示的区域为A,不等式组
表示的区域为A,不等式组 表示的区域为B,在区域A中任意取一点P
表示的区域为B,在区域A中任意取一点P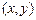 .
.
(Ⅰ)求点P落在区域B中的概率;
(Ⅱ)若 分别表示甲、乙两人各掷一次正方体骰子所得的点数,求点P落在区域B中的概率.
分别表示甲、乙两人各掷一次正方体骰子所得的点数,求点P落在区域B中的概率.
已知圆 经过
经过 和直线
和直线 相切,且圆心在直线
相切,且圆心在直线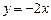 上.
上.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)若直线 经过圆
经过圆 内一点
内一点 与圆
与圆 相交于
相交于 两点,当弦
两点,当弦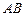 被点
被点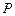 平分时,求直线
平分时,求直线 的方程
的方程
某小区要建一座八边形的休闲小区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200 m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如ΔDQH等)上铺草坪,造价为80元/m2。
设总造价为S元,AD长为xm,试建立S与x的函数关系;
当x为何值时,S最小?并求这个最小值。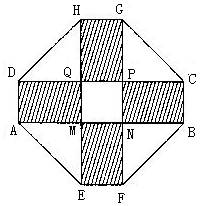
已知:在函数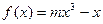 的图象上,以
的图象上,以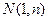 为切点的切线的倾斜角为
为切点的切线的倾斜角为
(I)求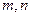 的值;
的值;
(II)是否存在最小的正整数 ,使得不等式
,使得不等式 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数 ,如果不存在,请说明理由。
,如果不存在,请说明理由。