在Rt△ABC中,∠ACB=30°,∠B=90°,D为AC中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角A-BD-C大小记为θ.
(Ⅰ)求证:面AEF⊥面BCD;
(Ⅱ)θ为何值时,AB⊥CD. 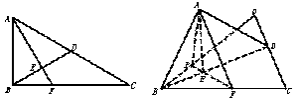
(本小题满分14分)已知定义域为 的函数
的函数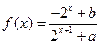 是奇函数。
是奇函数。
(Ⅰ)求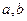 的值;
的值;
(Ⅱ)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求
 的取值范围;
的取值范围;
(本小题满分14分)
已知条件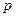 :
: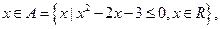
条件 :
: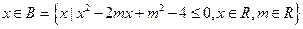
(Ⅰ)若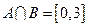 ,求实数
,求实数 的值;
的值;
(Ⅱ)若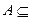
 ,求实数
,求实数 的取值范围.
的取值范围.
已知椭圆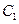 、抛物线
、抛物线 的焦点均在
的焦点均在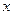 轴上,
轴上,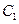 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
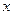 |
3 |
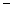 2 2 |
4 |
 |
 |
 |
0 |
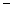 4 4 |
 |
(Ⅰ)求 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线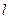 满足条件:①过
满足条件:①过 的焦点
的焦点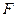 ;②与
;②与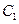 交不同两点
交不同两点 且满足
且满足 ?若存在,求出直线
?若存在,求出直线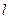 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本小题满分12分)
已知函数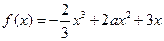 .
.
(Ⅰ)当 时,求函数
时,求函数 在
在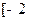 ,
, 上的最大值、最小值;
上的最大值、最小值;
(Ⅱ)令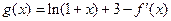 ,若
,若 在
在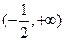 上单调递增,求实数
上单调递增,求实数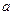 的取值范围.
的取值范围.
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从 道备选题中一次性抽取
道备选题中一次性抽取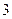 道题独立作答,然后由乙回答剩余
道题独立作答,然后由乙回答剩余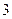 题,每人答对其中
题,每人答对其中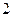 题就停止答题,即闯关成功.已知在
题就停止答题,即闯关成功.已知在 道备选题中,甲能答对其中的
道备选题中,甲能答对其中的 道题,乙答对每道题的概率都是
道题,乙答对每道题的概率都是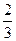 .
.
(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设甲答对题目的个数为ξ,求ξ的分布列及数学期望.