某校从参加高三年级第一学期期末考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数，满分为100分），将数学成绩进行分组并根据各组人数制成如下频率分布表：
（Ⅰ）将上面的频率分布表补充完整，并估计本次考试全校85分以上学生的比例；
（Ⅱ）为了帮助成绩差的同学提高数学成绩，学校决定成立“二帮一”小组，即从成绩为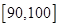
中任出两位同学，共同帮助成绩在
中的某一个同学，试列出所有基本事件；若
同学成绩为43分，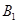
同学成绩为95分，求、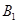两同学恰好被安排在“二帮一”中同一小组的概率．
| 分组 |
频数 |
频率 |
| [ 40, 50 ） |
2 |
0.04 |
| [ 50, 60 ） |
3 |
0.06 |
| [60, 70 ） |
14 |
0.28 |
| [ 70, 80 ） |
15 |
0.30 |
| [ 80, 90 ） |
|
|
| [ 90, 100 ] |
4 |
0.08 |
| 合计 |
|
|
过抛物线y2=2px（p＞0）的对称轴上的定点M（m,0）（m＞0）,作直线AB与抛物线相交于A,B两点.
（1）试证明A,B两点的纵坐标之积为定值；
（2）若点N是定直线l：x=－m上的任意一点,分别记直线AN,MN,BN的斜率为k1,k2,k3,试探求k1,k2,k3之间的关系,并给出证明.
设
上的两点，已知向量
，
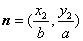,若m·n=0且椭圆的离心率
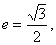短轴长为2，
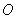为坐标原点．
（Ⅰ）求椭圆的方程；
（Ⅱ）若直线AB过椭圆的焦点F（0，c），（c为半焦距），求直线AB的斜率k的值；
（Ⅲ）试问：△AOB的面积是否为定值？如果是，请给予证明；如果不是，请说明理由.
是经过椭圆
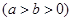右焦点的任一弦，若过椭圆中心Ｏ的弦
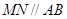，求证：
：
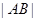是定值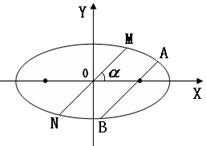
已知定点
在抛物线
：
（
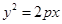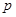＞0）上，动点
且
．求证：弦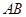
必过一定点．
已知,椭圆C经过点A（1,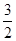
）,两个焦点为（－1,0）,（1,0）．
（1）求椭圆C的方程；
（2）E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.