设 上的两点,已知向量
上的两点,已知向量 ,
,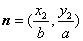 ,若m·n=0且椭圆的离心率
,若m·n=0且椭圆的离心率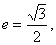 短轴长为2,
短轴长为2,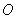 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线AB过椭圆的焦点F(0,c),(c为半焦距),求直线AB的斜率k的值;
(Ⅲ)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
已知 =(cos2
=(cos2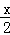 ,
,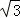 sinx),
sinx),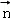 =(2,1),设函数f(x)=
=(2,1),设函数f(x)=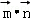 .
.
(1)当x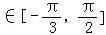 ,求函数f(x)的值域;
,求函数f(x)的值域;
(2)当f(α)= ,且﹣
,且﹣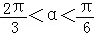 ,求sin(2
,求sin(2 )的值.
)的值.
已知函数f(x)=x2+|x﹣a|.
(1)当a=1时,求函数f(x)的最小值;
(2)试讨论函数f(x)的奇偶性,并说明理由.
公差不为零的等差数列{an}中,a1、a2、a5成等比数列,且该数列的前10项和为100.
(1)求数列{an}的通项公式;
(2)若bn=an﹣10,求数列{bn}的前n项和Tn的最小值.
对定义在[0,1]上的函数f(x),如果同时满足以下三个条件:
①对任意x∈[0,1],总有f(x)≥0;
②f(1)=1;
③若x1≥0,x2≥0,x1+x2≤1,有f(x1+x2)≥f(x1)+f(x2)成立.
则称函数f(x)为理想函数.
(1)判断g(x)=2x﹣1(x∈[0,1])是否为理想函数,并说明理由;
(2)若f(x)为理想函数,求f(x)的最小值和最大值;
(3)若f(x)为理想函数,假设存在x0∈[0,1]满足f[f(x0)]=x0,求证:f(x0)=x0.
已知椭圆E的长轴长与焦距比为2:1,左焦点F(﹣2,0),一定点为P(﹣8,0).
(1)求椭圆E的标准方程;
(2)过P的直线与椭圆交于P1、P2两点,设直线P1F、P2F的斜率分别为k1、k2,求证:k1+k2=0.
(3)求△P1P2F面积的最大值.