对定义在[0,1]上的函数f(x),如果同时满足以下三个条件:
①对任意x∈[0,1],总有f(x)≥0;
②f(1)=1;
③若x1≥0,x2≥0,x1+x2≤1,有f(x1+x2)≥f(x1)+f(x2)成立.
则称函数f(x)为理想函数.
(1)判断g(x)=2x﹣1(x∈[0,1])是否为理想函数,并说明理由;
(2)若f(x)为理想函数,求f(x)的最小值和最大值;
(3)若f(x)为理想函数,假设存在x0∈[0,1]满足f[f(x0)]=x0,求证:f(x0)=x0.
在锐角△ABC中,cos B+cos (A-C)=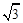 sin C.
sin C.
(Ⅰ) 求角A的大小; (Ⅱ) 当BC=2时,求△ABC面积的最大值.
已知函数 .
.
(Ⅰ)当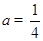 时,求函数
时,求函数 在
在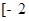 ,
,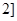 上的最大值、最小值;
上的最大值、最小值;
(Ⅱ)令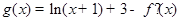 ,若
,若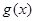 在
在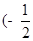 ,
, 上单调递增,求实数
上单调递增,求实数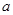 的取值范围.
的取值范围.
已知函数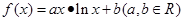 ,在点
,在点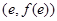 处的切线方程是
处的切线方程是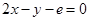 (e为自然对数的底)。
(e为自然对数的底)。
(1)求实数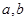 的值及
的值及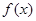 的解析式;
的解析式;
(2)若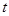 是正数,设
是正数,设 ,求
,求 的最小值;
的最小值;
(3)若关于x的不等式 对一切
对一切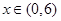 恒成立,求实数
恒成立,求实数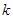 的取值范围.
的取值范围.
在△ 中,角
中,角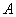 、
、 、
、 所对的边分别为
所对的边分别为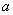 、
、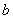 、
、 ,且
,且 .
.
(Ⅰ)若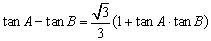 ,求角
,求角 ;
;
(Ⅱ)设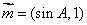 ,
, ,试求
,试求 的最大值.
的最大值.
已知不等式 的解集为A,函数
的解集为A,函数 的定义域为B.
的定义域为B.
(Ⅰ)若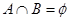 ,求
,求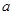 的取值范围;
的取值范围;
(Ⅱ)证明:函数 的图象关于原点对称。
的图象关于原点对称。