(本小题满分12分)数列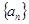 ,
, 的每一项都是正数,
的每一项都是正数,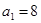 ,
, ,且
,且 ,
,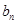 ,
,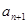 成等差数列,
成等差数列,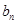 ,
,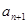 ,
,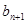 成等比数列,
成等比数列, .
.
(Ⅰ)求 ,
,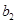 的值;
的值;
(Ⅱ)求数列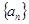 ,
, 的通项公式;
的通项公式;
(Ⅲ)证明:对一切正整数 ,有
,有 .
.
(本小题满分12分)已知 .
.
(1)是否存在常数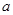 、
、 ,使得
,使得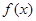 的值域为
的值域为 ?若存在,求出
?若存在,求出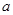 、
、 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(2)在(1)的条件下,求函数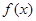 的单调区间.
的单调区间.
(本小题满分12分)如下图,某地一天从 时到
时到 时的温度变化曲线近似满足函数
时的温度变化曲线近似满足函数
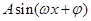 ,
, .
.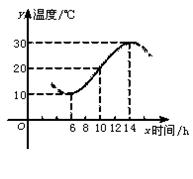
(1)写出这段曲线的函数 的解析式;
的解析式;
(2)当 时,若函数
时,若函数 是偶函数,求实数
是偶函数,求实数 的最小值.
的最小值.
(本小题满分12分)已知函数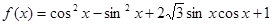 .
.
(1)求 的最小正周期,并求
的最小正周期,并求 的最小值及此时x的取值集合;
的最小值及此时x的取值集合;
(2)若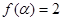 ,且
,且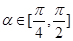 ,求
,求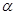 的值.
的值.
(本小题满分12分)设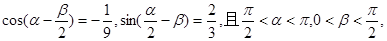
求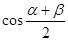 的值.
的值.
(本小题满分12分)青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
| 分组 |
频数 |
频率 |
| [50,60) |
2 |
0.04 |
| [60,70) |
8 |
0.16 |
| [70,80) |
10 |
|
| [80,90) |
||
| [90,100] |
14 |
0.28 |
| 合计 |
1.00 |
(1)填写答题卡上频率分布表中的空格,并补全频率分布直方图;
(2)试估计该年段成绩在[70,90)段的有多少人?
(3)请你估算该年段的平均分.