如图,圆 与圆
与圆 交于
交于 两点,以
两点,以 为切点作两圆的切线分别交圆
为切点作两圆的切线分别交圆 和圆
和圆 于
于 两点,延长
两点,延长 交圆
交圆 于点
于点 ,延长
,延长 交圆
交圆 于点
于点 .已知
.已知 .
.
(1)求 的长;
的长;
(2)求 .
.
(本小题满分10分)已知函数 为偶函数,且在
为偶函数,且在 上为增函数.
上为增函数.
(1)求 的值,并确定
的值,并确定 的解析式;
的解析式;
(2)若 且
且 ,是否存在实数
,是否存在实数 使
使 在区间
在区间 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题满分10分)已知直线 经过点
经过点 ,且和圆
,且和圆 相交,截得的弦长为4
相交,截得的弦长为4 ,求直线
,求直线 的方程.
的方程.
(本小题满分10分)某企业拟投资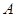 、
、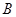 两个项目,预计投资
两个项目,预计投资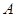 项目
项目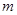 万元可获得利润
万元可获得利润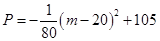
万元;投资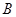 项目
项目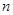 万元可获得利润
万元可获得利润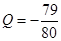
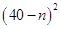
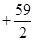
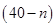 万元.若该企业用40
万元.若该企业用40
万元来投资这两个项目,则分别投资多少万元能获得最大利润?最大利润是多少?
(本小题满分10分)如图,四边形ABCD是正方形,O是正方形的中心,PO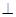 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.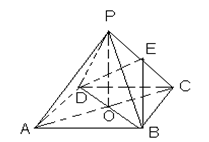
求证:(1) PA∥平面BDE .
(2)平面PAC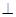 平面BDE .
平面BDE .
(本小题满分8分)已知直线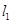 :
: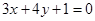 和点
和点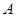 (1,2),设过
(1,2),设过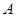 点与
点与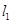 垂直的直线为
垂直的直线为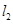 .
.
(1)求直线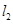 的方程;
的方程;
(2)求直线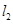 与两坐标轴围成的三角形的面积.
与两坐标轴围成的三角形的面积.