
如图所示,质量为3m的足够长木板C 静止在光滑水平面上,质量均为m 的两个物体A、B 放在C 的左端,A、B 间相距s0,现同时对A、B施加水平向右的瞬间冲量而使之分别获得初速度v0和2v0,若A、B与C之间的动摩擦因数分别为μ 和2 μ ,则:
(1)最终A、B、C的共同速度为多大
(2)求A达到最小速度时,系统产生的热量Q。
如图,空间中存在两条射线OM、ON,以及沿射线OM方向的匀强电场,已知∠NOM=θ,某带电粒子从射线OM上的某点P垂直于OM入射,仅在电场作用下经过射线ON上的Q点,若Q点离O点最远且OQ=L,求(1)粒子入射点P离O点的距离S。
(2)带电粒子经过电压U加速后从P点入射,则改变电压U时,欲使粒子仍然能经过Q点,试画出电压U与匀强电场的场强E之间的关系。(只定性画出图线,无需说明理由)
如图(a)所示,在足够长的光滑水平面上,放置一长为L=1m、质量为m1=0.5kg的木板A,一质量为m2=1kg的小物体B以初速度v0滑上A的上表面的同时对A施加一个水平向右的力F,A与B之间的动摩擦因数为μ=0.2,g=10m/s2;小物体B在A上运动的路程S与F力的关系如图(b)所示。求:v0、F1、F2。
如图7所示,一个光滑的弧形槽AB与水平粗糙轨道BC面相连接,另一圆形光滑轨道竖直放置与BC相切于C点,小球在离地面高h=0.45m的A点沿弧形槽静止开始滑下,进入水平轨道BC后,再进入圆形轨道内。已知小球在BC段动摩擦因数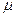 =0.25,BC长度为L=1m,圆形轨道半径为r=0.1m,g取l0m/s2,求:
=0.25,BC长度为L=1m,圆形轨道半径为r=0.1m,g取l0m/s2,求: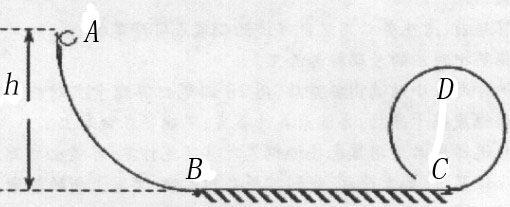
(1)小球滑到B点时和C点时的速度大小;
(2)要使小球能达到圆轨道的最高点D处,则小球在A速度至少为多少?
我国在2007年10月发射一颗绕月运行的探月卫星“嫦娥1号”。设“嫦娥1号”卫星环绕月球做圆周运动,在此圆轨道上运行周期为T。已知探月卫星轨道半径为R,引力常数为G。试求出:
(1)月球的质量;
(2)若月球表面的重力加速度为g,求月球的半径。