求下列函数的导数（其中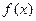
是可导函数）
；
三棱柱ABC—A1B1C1中，侧棱与底面垂直,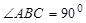
，
,
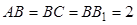分别是
,
的中点．
（1）求直线MN与平面A1B1C所成的角；
（2）在线段AC上是否存在一点E，使得二面角E-B1A1-C的余弦值为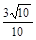
?若存在，求出AE的长，若不存在，请说明理由.
已知P：方程x2+mx+1=0有两个不等的负根；q:方程 4x2+4(m-2)x+1=0
无实根.若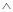p
q为假，p
q为真，求m的取值范围.
已知f (x)=2x－
（1）若f (x)=2，求x的值.
（2）若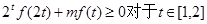
恒成立，求实数m的取值范围.
变量x、y满足
（1）假设z =4x－3y，求z的最大值.
（2）设z =
，求z的最小值.
（3）设z =x2+y2，求z的取值范围.
在自然数集N上定义一个函数y = f (x)，已知f (1) + f (2)=5.当x为奇数时，f (x+1)－f (x)=1，当x为偶数时f (x+1)－f (x)=3.
（1）求证：f (1)，f (3)，f (5)，……，f (2n－1) （n∈N+）成等差数列.
（2）求f (x)的解析式.