已知 ,点A(s,f(s)), B(t,f(t))
,点A(s,f(s)), B(t,f(t))
(I) 若 ,求函数
,求函数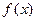 的单调递增区间;
的单调递增区间;
(II)若函数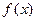 的导函数
的导函数 满足:当|x|≤1时,有|
满足:当|x|≤1时,有| |≤
|≤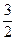 恒成立,求函数
恒成立,求函数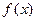 的解析表达式;
的解析表达式;
(III)若0<a<b, 函数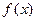 在
在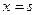 和
和 处取得极值,且
处取得极值,且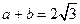 ,证明:
,证明: 与
与 不可能垂直.
不可能垂直.
已知 、
、 、
、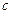 分别是△ABC的三个内角A、B、C的对边,设
分别是△ABC的三个内角A、B、C的对边,设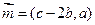 ,
,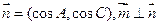 .
.
(1)求角A的大小; (2)若 ,求
,求 的值.
的值.
(本小题満分14分)
已知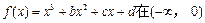 上是增函数,在[0,2]上是减函数,且方程
上是增函数,在[0,2]上是减函数,且方程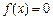 有三个根,它们分别为
有三个根,它们分别为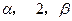 .
.
(1)求c的值;
(2)求证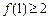 ;
;
(3)求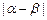 的取值范围.
的取值范围.
已知点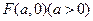 ,动点
,动点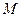 、
、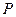 分别在
分别在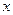 、
、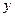 轴上运动,满足
轴上运动,满足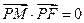 ,
,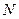 为动点,并且满足
为动点,并且满足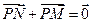 .
.
(1)求点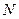 的轨迹
的轨迹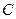 的方程;
的方程;
(2)过点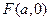 的直线
的直线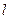 (不与
(不与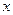 轴垂直)与曲线
轴垂直)与曲线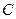 交于
交于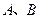 两点,设点
两点,设点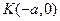 ,
,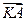 与
与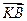 的夹角为
的夹角为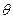 ,求证:
,求证: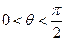 .
.
如图,已知直角梯形 的上底
的上底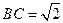 ,
,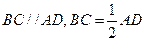 ,
,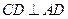 ,平面
,平面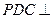 平面
平面 ,
,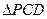 是边长为
是边长为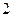 的等边三角形。
的等边三角形。
(1)证明: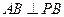 ;
;
(2)求二面角 的大小。
的大小。
(3)求三棱锥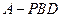 的体积。
的体积。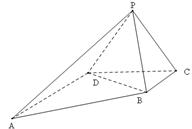
已知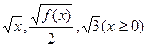 成等差数列.又数列
成等差数列.又数列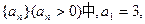 此数列的前n项的和Sn(
此数列的前n项的和Sn(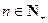 )对所有大于1的正整数n都有
)对所有大于1的正整数n都有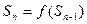 .
.
(1)求数列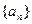 的第n+1项;
的第n+1项;
(2)若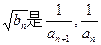 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn.