已知函数
在区间[0，1]上单调递增，在区间[1，2]上单调递减；
（1）求a的值；
（2）求证：x=1是该函数的一条对称轴；
（3）是否存在实数b，使函数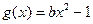
的图象与函数f(x)的图象恰好有两个交点？若存在，求出b的值；若不存在，请说明理由.
如图，在正四棱台
中，
，
，
，
、
分别是
、
的中点. 
（Ⅰ）求证：平面
∥平面
；
（Ⅱ）求二面角
的余弦值的大小.
注：底面为正方形，从顶点向底面作垂线，垂足是底面中心，这样的四棱锥叫做正四棱锥.用一个平行于正四棱锥底面的平面去截该棱锥，底面与截面之间的部分叫做正四棱台.
为了分流地铁高峰的压力，某市发改委通过听众会，决定实施低峰优惠票价制度.不超过
公里的地铁票价如下表：
乘坐里程 （单位： ） |
 |
 |
 |
| 票价（单位：元） |
 |
 |
 |
现有甲、乙两位乘客，他们乘坐的里程都不超过公里.已知甲、乙乘车不超过
公里的概率分别为
，
，甲、乙乘车超过公里且不超过
公里的概率分别为
，.
（Ⅰ）求甲、乙两人所付乘车费用不相同的概率；
（Ⅱ）设甲、乙两人所付乘车费用之和为随机变量
，求的分布列与数学期望．
已知向量
,
,实数
为大于零的常数，函数
,
，且函数
的最大值为
.
（Ⅰ）求的值；
（Ⅱ）在
中，
分别为内角
所对的边，若
，
,且
,求
的最小值.
（本小题满分10分）
已知集合A是集合Pn＝{1，2，3， ，n} (n≥3，n∈N*)的子集，且A中恰有3个元素，同时这3个元素的和是3的倍数．记符合上述条件的集合A的个数为f(n)．
（1）求f(3)，f(4)；
（2）求f(n)（用含n的式子表示）．
（本小题满分10分）
如图，四棱锥P－ABCD中，PA^平面ABCD，AD∥BC，AB^AD，BC＝，AB＝1，BD＝PA＝2．
（1）求异面直线BD与PC所成角的余弦值；
（2）求二面角A－PD－C的余弦值．