(本小题满分14分)已知函数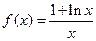
(1)若函数在区间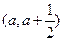 其中a >0,上存在极值,求实数a的取值范围;
其中a >0,上存在极值,求实数a的取值范围;
(2)如果当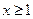 时,不等式
时,不等式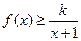 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(3)求证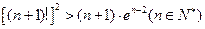 .
.
(本小题满分14分)椭圆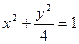 短轴的左右两个端点分别为A,B,直线
短轴的左右两个端点分别为A,B,直线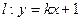 与x轴、y轴分别交于两点E,F,交椭圆于两点C,D。
与x轴、y轴分别交于两点E,F,交椭圆于两点C,D。
(I)若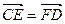 ,求直线
,求直线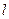 的方程; (II)设直线AD,CB的斜率分别为
的方程; (II)设直线AD,CB的斜率分别为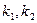 ,若
,若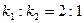 ,求k的值。
,求k的值。
(本小题满分12分)已知函数 ,数列
,数列 满足
满足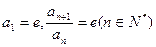 .
.
(Ⅰ)求数列 的通项公式
的通项公式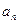 ;
;
(Ⅱ)求 ;
;
(Ⅲ)求证:
(本小题满分12分)经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为 .
.
(Ⅰ)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?
(Ⅱ)若要求在该时段内车流量超过9千辆/小时,则汽车的平均速度应在什么范围内?
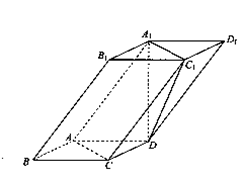
(本小题满分12分)如图,已知四棱柱ABCD—A1B1C1D1中,A1D⊥底面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2。
(I)求证:C1D//平面ABB1A1;
(II)求直线BD1与平面A1C1D所成角的正弦值;
(Ⅲ)求二面角D—A1C1—A的余弦值。